capitaine nuggets a écrit:On a bien définie l'exponentielle complexe :
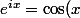+i \sin(x))
avec

réel.
En fait l'exponentielle est définie par e^x = 1 + x + x*x/2! + x*x*x/3! + x*x*x*x/4! + ... dans tout un tas de contextes (par exemple, exponentielles de matrices).
On peut aussi la définir comme étant l'unique application dérivable de C dans C telle que exp(0) = 1 et exp'(x) = exp(x)
Ensuite on regarde e^(ix) (lui son équadiff c'est y' = iy) et on se rend compte que quand on marche dans une direction orthogonale au segment qui nous relie à 0, eh ben on marche à vitesse constante en cercle autour de 0. Donc on peut définir pi comme étant le plus petit réel > 0 tel que exp(2ipi) = 1 (c'est la distance parcourue pour revenir au point de départ donc 2pi = la circonférence du cercle de rayon 1)
C'est ensuite qu'on définit cos et sin (2cos(x) = exp(ix) + exp(-ix) et 2isin(x) = exp(ix) - exp(-ix), pour x dans C ; ou bien cos(x) = Re(exp(x)) et sin(x)= Im(exp(x)), pour x dans R). Ou alors en donnant les équadiffs correspondantes si on préfère définir les gens en équadiff.
Pour z^i et log, soit tu définis log autour de 1 par une série entière (mais ça ne te définit log que dans un disque de rayon 1 autour de 1, donc c'est pas chouette)
soit comme solution d'une équation différentielle sur un ouvert à préciser qui risque pas de contenir 0. Les équations différentielles en question, (les solutions de zf'(z) = if(z) ; et de zf'(z) = 1 respectivement) se comportent mal en 0
Sinon tu définis pas log et à la place tu dis juste "soit x un complexe tel que e^x = i" plutot que "soit x = log(i)". Et tu définis pas z^i mais par contre tu regardes le sous-ensemble de C² {(exp(x),exp(ix)}, qui ressemble fort à ce que serait le graphe d'une fonction qui voudrait être z^i.
Enfin i^i on en parle pas, mais par contre on peut regarder dans {(exp(x),exp(ix))}, l'ensemble des points dont la première coordonnée est i. Il y en a pas mal.
Bref, il ne faut jamais jamais jamais JAMAIS JAMAIS utiliser "^" avec des complexes.
avec
réel.