Dérivabilité d'une fonction

[klink60]

Bonsoir,

je dois montrer que la fonction f définie sur R ainsi :

si et sinon

est dérivable sur R

Je dois donc montrer que :
1. un réel
2. un réel

Je n'arrive pas à trouver ces deux limites FI de type 0/0 ...

Merci d'avance pour votre aide
J'attends vos réponses ! :help:

[Arnaud-29-31]

Bonsoir,

Es-tu sûr que les limites que tu proposes doivent être juste égales à n'importe quel réel bon pouvoir conclure ?

On doit normalement s'en sortir avec le théorème des croissances comparées.

[mathelot]

salut,

poser x=1-h avec h>0 qd x tend vers 1

tend vers 0 qd h tend vers 0+
pour n'importe quel polynôme P

ça devrait aider à récurrer

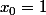
cette fonction est un exemple célèbre: série de Taylor convergente en mais pas vers la fonction