Derivabilite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 18 Déc 2015, 21:09
par biss » 18 Déc 2015, 21:09
Salut à tous, je vous présente aujourd'hui ce problème
Pour

on a
=\frac{1+x^n}{(1+x)^n})
définie de R+ vers R, pour tout
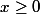
1) montrer que f est dérivable sur R+ et calculé f'(x) pour x;)0
Je pense déjà connaitre la réponse
-f(0)}{x-0}=l)
donc f est dérivable sur R+ enfin c'est ce que j'ai l'habitude de faire mais sans comprendre vraiment pourquoi je ne vérifie pas les autres valeurs dans R+
Si quelqu'un pouvais l'éclaircir
-
remullen2000
- Membre Relatif
- Messages: 167
- Enregistré le: 28 Mar 2008, 18:52
-
 par remullen2000 » 18 Déc 2015, 21:21
par remullen2000 » 18 Déc 2015, 21:21
Bonsoir,
Attention, ce n'est pas n qui doit tendre vers 2 mais x qui doit tendre vers 0.
De plus en pratique on utilise rarement la définition, il suffit de dire qu'il s'agit de composées de fonctions toutes dérivables pour tout n.
Ensuite tu utilises la formule de la dérivée d'un quotient.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Déc 2015, 21:31
par aymanemaysae » 18 Déc 2015, 21:31
Si vous avez un peu de temps, vous trouverez que c'est agréable d'essayer de démontrer que f est dérivable sur IR+ en utilisant la définition.
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 18 Déc 2015, 22:04
par biss » 18 Déc 2015, 22:04
??Je n'arrive à faire le lien avec ma question ?_?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Déc 2015, 22:17
par aymanemaysae » 18 Déc 2015, 22:17
Le chemin le plus court et le plus pratique est celui indiqué par M. remullen2000: ma proposition était pour vous inviter à sonder d'autres sentiers comme celui qui consiste à utiliser la définition de la dérivée, même si ce n'est pas très pratique.
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 18 Déc 2015, 23:06
par biss » 18 Déc 2015, 23:06
En gros ce que j'ai fais est faux ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Déc 2015, 23:16
par Ben314 » 18 Déc 2015, 23:16
Si c'est de ça que tu parle :
biss a écrit:-f(0)}{x-0}=l) donc f est dérivable sur R+
donc f est dérivable sur R+
C'est effectivement n'importe quoi.
Au mieux, si tu avait écrit x->0 (a la place de n->0) ET si tu avait justifié que la limite en question existe (là, il n'y a rien dans ce que tu écrit qui explique pourquoi cette limite existe, ni quelle est la valeur de cette limite), alors ça prouverais uniquement que f est dérivable en 0 et rien d'autre.
Donc tel quel, ça ne vaut rien : une affirmation gratuite (i.e. sans preuve) + une conclusion erronée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 19 Déc 2015, 09:46
par zygomatique » 19 Déc 2015, 09:46
salut
il me semble que dans le supérieur il suffit de dire que f est une fraction rationnelle donc est dérivable sur son ensemble de définition ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 19 Déc 2015, 11:47
par biss » 19 Déc 2015, 11:47
Fraction rationnelle ? Tu peux m'expliquee mieux ?
Sinon c'est la ccomposé de quelle fonction dérivable ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2015, 13:12
par Ben314 » 19 Déc 2015, 13:12
Normalement (???) tu as du apprendre en terminale que la somme, le produit et le quotient (avec dénominateur non nul) de fonctions dérivables est dérivable [plus les formules de dérivations correspondantes] ET que certaines fonction "de référence" sont dérivable sur certains ensembles.
Par exemple, tu es sensé savoir que tout polynôme est dérivable sur R tout entier donc en particulier que x->1+x^n et x->(1+x)^n sont dérivables sur R et tu en déduit que le quotient (1+x^n)/(1+x)^n est dérivable partout où le dénominateur est non nul, donc sur R-{-1}.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 19 Déc 2015, 13:59
par biss » 19 Déc 2015, 13:59
Oui j'avais appris cela mais peut être j'étais dans les vagues quand on me parlais du quotient sinon je sais déjà pour le produit et la somme. Merci j'ai compris

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2015, 14:41
par Ben314 » 19 Déc 2015, 14:41
Ca métonnerais fort que tu n'ait jamais utilisé
'=\cdots)
et le théorème donnant cette formule, il commence
forcément par dire que

est dérivable lorsque

et

le sont (et que
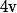
ne sannule pas sur le domaine d'étude)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
biss
- Membre Rationnel
- Messages: 659
- Enregistré le: 30 Oct 2015, 18:02
-
 par biss » 19 Déc 2015, 14:54
par biss » 19 Déc 2015, 14:54
Ben314 a écrit:Ca métonnerais fort que tu n'ait jamais utilisé
'=\cdots)
et le théorème donnant cette formule, il commence
forcément par dire que

est dérivable lorsque

et

le sont (et que
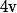
ne sannule pas sur le domaine d'étude)
Je l'ai utilisé n^2 fois mais j'ai juste appris la forums sans le théorème le concernant, il est vrai que je préfère allez directement au but des chapitres mais finalement quelque années après l'avoir appris je viens de connaitre son histoire et pour les questions du type montrer que (u/v) est derdérivable bah je faisais comme je l'ai dis à mon 1er poste (je me suis trompé entre n et x ) et c'est parce que aujourd'hui j'ai su cela bizzare que je pose cette question
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 19 Déc 2015, 17:15
par Pythales » 19 Déc 2015, 17:15
biss a écrit:Salut à tous, je vous présente aujourd'hui ce problème
Pour

on a
=\frac{1+x^n}{(1+x)^n})
définie de R+ vers R, pour tout
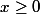
1) montrer que f est dérivable sur R+ et calculé f'(x) pour x;)0
Je pense déjà connaitre la réponse
-f(0)}{x-0}=l)
donc f est dérivable sur R+ enfin c'est ce que j'ai l'habitude de faire mais sans comprendre vraiment pourquoi je ne vérifie pas les autres valeurs dans R+
Si quelqu'un pouvais l'éclaircir
Si tu tiens absolument à revenir à la définition :
-f(x)}h=\frac1h\left(\frac{1+(x+h)^n}{(1+x+h)^n}-\frac{1+x^n}{(1+x^n}\right)=\frac{(1+x)^n+(x+h)^n(1+x^n)-(1+x+h)^n-x^n(1+x+h)^n}{h(1+x+h)^n(1+x)^n})
^n+(x^n+nhx^{n-1}+O(h^2))(1+x^n)-(1+x)^n+nh(1+x)^{n-1}+O(h^2)-x^n[(1+x)^n+nh(1+x)^{n-1}+O(h^2)]}{h(1+x+h)^n(1+x)^n}=\frac{nhx^{n-1}(1+x^n)-nh(1+x)^{n-1}-nhx^n(1+x)^{n-1}+O(h^2)}{h(1+x+h)^n(1+x)^n})
et si
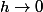
cette expression tend vers
^n-n(1+x)^{n-1}(1+x^n)}{(1+x)^{2n}})
qui peut encore se simplifier ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
donc f est dérivable sur R+
et le théorème donnant cette formule, il commence forcément par dire que
est dérivable lorsque
et
le sont (et que
ne sannule pas sur le domaine d'étude)
on a
définie de R+ vers R, pour tout
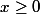
donc f est dérivable sur R+ enfin c'est ce que j'ai l'habitude de faire mais sans comprendre vraiment pourquoi je ne vérifie pas les autres valeurs dans R+