Dépend d'un représenant ?

[zenaf]

Bonjour,

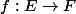
Soit avec E un ensemble quotient.

Vérifier que f ne dépend pas du représentant choisi. Que cela signifie t'il ?

[Nightmare]

Salut :happy3:

Un ensemble quotient, c'est un ensemble de classes d'équivalences pour une certaine relation R. Une classe d'équivalence qu'est-ce? Pour un élément x choisit, la classe d'équivalence de x est l'ensemble des éléments en relation avec x. On se rend compte alors que les classes de chacun de ces éléments sont toutes égales à la classe de x. On peut donc "représenter" toutes ces classes d'équivalences arbitrairement par l'un quelconque des éléments, appelé alors représentant.

Par exemple, on considère la relation de congruence modulo 3. Les classes d'équivalences de 1, 4, 7, 10 etc... sont toutes les même. 1, 4, 7 et 10 en sont des représentant.

[zenaf]

Salut :happy3:

Un ensemble quotient, c'est un ensemble de classes d'équivalences pour une certaine relation R. Une classe d'équivalence qu'est-ce? Pour un élément x choisit, la classe d'équivalence de x est l'ensemble des éléments en relation avec x. On se rend compte alors que les classes de chacun de ces éléments sont toutes égales à la classe de x. On peut donc "représenter" toutes ces classes d'équivalences arbitrairement par l'un quelconque des éléments, appelé alors représentant.

Par exemple, on considère la relation de congruence modulo 3. Les classes d'équivalences de 1, 4, 7, 10 etc... sont toutes les même. 1, 4, 7 et 10 en sont des représentant.

Merci de la réponse mais ca je sais déjà.

Vérifier que f ne dépend pas du représentant choisi. Que cela signifie t'il ?

[SergeM]

En un mot si x et y sont dans la même classe d'équivalence, est-ce que f(x)=f(y)? (c'est ce que tu doit verifier (sinon ton application f n'a pas de sens)).

[catharaxie]

Si x,y et z sont des representants d'une meme classe d'equivalence, x=y=z mod(R) d'où f(x)=f(y)=f(z)