Densité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 08 Sep 2007, 19:32
par Pythix » 08 Sep 2007, 19:32
Bonjour,
j'ai un exercice qui me pose problème :
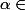
R\Q Montrer que N +

Z est dense dans

je ne vois pas trop comment faire...
Merci d'avance
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 08:56
par Pythix » 09 Sep 2007, 08:56
Peut on dire :
soit
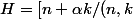\in N *Z])
sous groupe de

et montrer que H ne peut etre de la forme aZ donc H est dense dans R... ?
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 09 Sep 2007, 09:59
par Yipee » 09 Sep 2007, 09:59
Montrer que

est dense est très classique. On peut procéder comme tu le dis en disant que H est un sous groupe additif de R. Ensuite, on regarde le sup de

et on montre que c'est 0. On en déduit que H est dense.
Il faut peut-être adapter un peu. Dans ta version,

n'est plus un sous-groupe.
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 10:08
par Pythix » 09 Sep 2007, 10:08
oui, la première partie de l'exercice est Z+alphaZ
pour la deuxième avec N je bloque...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Sep 2007, 11:58
par yos » 09 Sep 2007, 11:58
Bonjour.
Adapte un peu la preuve de la caractérisation des sous-groupes de R.
Il te suffit de prouver que N+aZ renferme un élément arbitrairement proche de 0 (ça tu vois pourquoi?).
Pour ceci, tu peux regarder les réels a-E(a), 2a-E(2a),...na-E(na). Ils sont tous dans [0,1], tous distincts (pourquoi?), et donc avec le principe des tiroirs...
Si tu fais ta soustraction dans le bon sens, tu auras un élément de N+aZ.
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 13:08
par Pythix » 09 Sep 2007, 13:08
en fait je cherchais à appliquer :
si G sous groupe additif de R
alors soit G est dense dans R
soit G=aZ avec a élément de R+
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 13:22
par Pythix » 09 Sep 2007, 13:22
j'ai pas très bien compris pourquoi il fallait qu'il y ait un élément proche de 0, c'est une histoire d'adhérence non?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Sep 2007, 14:12
par yos » 09 Sep 2007, 14:12
Comme te l'a dit Yipee, N+aZ est pas un sous-groupe de R.
Si tu as un élément trés petit x>0 dans N+aZ, alors les réels nx où
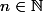
sont aussi dans N+aZ et forment un maillage serré de R+. C'est bien ce qu'on veut.
(Pour R-, il suffit de trouver y<0 arbitrairement voisin de 0 et dans N+aZ par la même méthode).
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 14:29
par Pythix » 09 Sep 2007, 14:29
donc on peut dire qu'il existe a, tel que à partir d'un certain rang N la suite
na-E(na) tend un élément de R, ce qui montrerait la densité??
-
Pythix
- Membre Relatif
- Messages: 134
- Enregistré le: 26 Oct 2005, 13:42
-
 par Pythix » 09 Sep 2007, 15:24
par Pythix » 09 Sep 2007, 15:24
et si on a prouvé que Z+alpha.Z est dense dans R comment se ramener à N+alpha.Z dense dans R ??
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 09 Sep 2007, 18:29
par Yipee » 09 Sep 2007, 18:29
yos a écrit:
Pour ceci, tu peux regarder les réels a-E(a), 2a-E(2a),...na-E(na). Ils sont tous dans [0,1], tous distincts (pourquoi?), et donc avec le principe des tiroirs...
Je ne vois pas trop comment conclure avec le principe des tiroirs....
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Sep 2007, 20:00
par yos » 09 Sep 2007, 20:00
Pour Pythix : mon "a" est ton "alpha". Je croyais que ça se voyait.
Salut Yipee. Mon idée est la suivante : d'après le principe des tiroirs, il existe i et j tels que
]-[ja-E(ja)]|<\epsilon)
, ce qu'on peut écrire
a- k|<\epsilon)
, où k est un entier. Selon le signe de k, l'un des réels (i-j)a-k ou son opposé est dans N+aZ et est

-proche de 0. Par contre, je n'ai pas le choix du côté de 0 : en tout cas j'ai la densité sur R+ ou sur R-. Il y a un défaut à corriger. J'y réfléchirai pour m'endormir.
-
Pavel
- Membre Relatif
- Messages: 119
- Enregistré le: 23 Déc 2005, 21:01
-
 par Pavel » 09 Sep 2007, 22:30
par Pavel » 09 Sep 2007, 22:30
On peut le faire d'une manière un peu plus bizarre
On prends Un = n et Vn = na - E(na)
L'ensemble {Up+Vq| (p,q) dans N*N} est dense dans R
(Ca se démontre par l'absurde)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Sep 2007, 11:56
par yos » 10 Sep 2007, 11:56
Sinon j'ai une autre idée, plus simple, sachant qu'on a déjà prouvé que Z+aZ est dense dans R.
Je pose
G=Z+aZ
E=N+aZ.
Soit
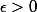
. On prend un élément g de G appartenant à
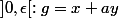
. Supposons que
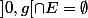
. Alors les éléments de

sont tous de la forme u+va avec ux. Il en existe donc au moins un : g'=u+va tel que
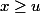
. L'élément g-g' est dans

ce qui est une contradiction.
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 10 Sep 2007, 12:00
par Yipee » 10 Sep 2007, 12:00
yos a écrit:Sinon j'ai une autre idée, plus simple, sachant qu'on a déjà prouvé que Z+aZ est dense dans R.
Je pose
G=Z+aZ
E=N+aZ.
Soit
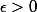
. On prend
deux éléments de G appartenant à

. On les soustrait dans le bon sens pour tomber dans E et on sera encore dans
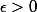
. Par Archimédisme, on a la densité de E dans R+.
On recommence pour R- .
Je pense que cette idée doit pouvoir fonctionner, mais il faut travailler plus. Rien ne permet ainsi d'affirmer que ta différence dans le sens qu'il faut pour être dans E ne soit pas toujours du même signe.
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 10 Sep 2007, 12:08
par Yipee » 10 Sep 2007, 12:08
Bon j'ai trouvé. On suppose par l'absurde que l'on ne peut pas trouver des éléments de E = N + aZ aussi proche que l'on veut de

. Par densité on construit une suite (u) strictement décroissante, tendant vers 0 d'éléments de G = Z+aZ. Par hypothèses, ce sont (à partir d'un certain rang) des éléments de F = Z_ + aZ. On pose
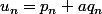
. Alors
 + a(q_n - q_{n+1}) \in F)
On en déduit que (p_n) est une suite strictement croissante ce qui est absurde car elle est à valeur dans

.
On fait pareil de l'autre coté.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Sep 2007, 12:12
par yos » 10 Sep 2007, 12:12
J'ai modifié mon truc. Je lis le tien.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Sep 2007, 12:14
par yos » 10 Sep 2007, 12:14
Bon on est en phase. Y compris dans les notations.
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 10 Sep 2007, 12:45
par Yipee » 10 Sep 2007, 12:45
yos a écrit:Bon on est en phase. Y compris dans les notations.
OK. A part deux trois fautes de frappes
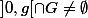
et les inégalités sont dans le mauvais sens car on travaille avec des nombres négatifs.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Sep 2007, 13:14
par yos » 10 Sep 2007, 13:14
Merci. j'ai corrigé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
. On prend deux éléments de G appartenant à
. On les soustrait dans le bon sens pour tomber dans E et on sera encore dans
. Par Archimédisme, on a la densité de E dans R+.