wilfred1995 a écrit:3. Combien y a-t-il de nombres formés de 4 chiffres distincts et qui soit multiple de 4?
pour le 3 c'est impossible
merci d'avance pour un bref contrôle.
Pour la 3, c'est faux.
Par exemple, 5364 est tout à fait divisible par 4.
Prenons un nombre à 4 chiffres

avec
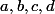
dans

Ce nombre est divisible par 4 si et seulement si

, soit

On cherche maintenant les nombres à 4 chiffres distincts divisibles par 4.
Déjà, faut être divisible par 2 donc les terminaisons possibles sont 0,2,4,6 ou 8.
Etudions les au cas par cas.
Si
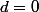
: ***0
Il faut que

donc

doit être pair et
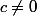
(car les 4 chiffres doivent être distincts) donc

soit 4 choix pour

.
Il y a ensuite 8 choix pour

et 7 choix pour

(les chiffres doivent être distincts) donc 56 choix possibles pour les deux premiers.
Il y a donc
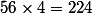
possibilités de multiples de 4 du style ***0.
Si
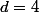
: ***4
Il faut que

, ce qui est équivalent à

pair une nouvelle fois.
Il y a donc 4 choix pour

.
Par contre, pour

et

, ce n'est plus la même. Il n'y a plus 56 choix car lorsque

, ça fait un nombre à 3 chiffres distincts au lieu de 3.
Il faut donc enlever les 7 choix qui conduisent à

.
On tombe alors sur 49 couples
)
avec
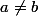
et
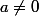
.
Mais quand c=0, la condition a=0 est impossible donc on dénombre 56 couples (a,b) tels que...
Ca fait donc au total :

nombres de ce type
Si
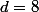
: ***8
Le même raisonnement conduit à 203 choix.
Si d=2 : ***2, on raisonne de même (en faisant attention à ne pas prendre a=0) et on trouve

choix.
Enfin, si
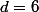
: ***6, le même raisonnement conduit aussi à 245 choix.
Bilan :
le nombre de nombres à 4 chiffres distincts multiples de 4 est :
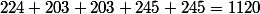
.
Un petit programme informatique (sur Python par exemple) permet de confirmer tout ça...
En espérant avoir été à peu près clair...

Sauf erreur.
Pseudo modifié : anciennement Trident2.
