Bonjour, cela doit être classique, mais je n'ai jamais rencontré cette situation.
Je lance 2 dés : (1;3), (2;2) et (3;1) 1+3=2+2=4 Du coup, 3 couples donnent une somme de 4.
je lance 3, 4, 5,..k dés: existe-il une technique pour dénombrer le nombre de k-uplets dont la somme des coordonnées vaille un entier donné? [bon, un algorithme va faire l'affaire mais sinon une formule générale?]
Merci.
Dénombrement
10 messages
- Page 1 sur 1
par capitaine nuggets » 15 Déc 2013, 14:57
Salut !
Si j'ai bien compris, en gros tu cherches le cardinal d'un ensemble de la forme :
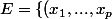\in \mathbb{[} 1,n\mathbb{]}^p\ {\rm tel\ que}\ \sum_{k=1}^p \ x_k = m,\ {\rm avec}\ m\in\mathbb{N}^* \})
jlb a écrit:Bonjour, cela doit être classique, mais je n'ai jamais rencontré cette situation.
Je lance 2 dés : (1;3), (2;2) et (3;1) 1+3=2+2=4 Du coup, 3 couples donnent une somme de 4.
je lance 3, 4, 5,..k dés: existe-il une technique pour dénombrer le nombre de k-uplets dont la somme des coordonnées vaille un entier donné? [bon, un algorithme va faire l'affaire mais sinon une formule générale?]
Merci.
Si j'ai bien compris, en gros tu cherches le cardinal d'un ensemble de la forme :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par jlb » 15 Déc 2013, 14:59
capitaine nuggets a écrit:Salut !
Si j'ai bien compris, en gros tu cherches le cardinal d'un ensemble de la forme :
oui c'est cela, et plus précisément n=6, on travaille avec un dé!
par capitaine nuggets » 15 Déc 2013, 15:41
jlb a écrit:oui c'est cela, et plus précisément n=6, on travaille avec un dé!
Ok, cherchons alors le cardinal de
Je n'ai pas vraiment de solution générale, mais je te propose ceci :
Pour
1- Quel est le cardinal de
2- Montre que l'application
3- Déduis-en alors le cardinal de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par jlb » 15 Déc 2013, 16:08
cherchons alors le cardinal de \in \{1,...,6\}^n\ {\rm tels\ que}\ \sum_{k=1}^n \ x_k=p\ {\rm avec}\ p\in\{n,...,6n\} \})
.
Je n'ai pas vraiment de solution générale, mais je te propose ceci :
Pour
, considérons l'ensemble \in \{1,...,6\}^n\ {\rm tels\ que}\ x_16 réponse 0; n=6 1<2<3<4<5<6 réponse 1; n=<5 réponse: 5!/(n!(5-n)!)<br /><br />2- Montre que l'application [TEX]f\ :\ E\to F)
définie par )=(x_1,x_1+x_2,...,x_1+... + x_n)))
est bijective.
3- Déduis-en alors le cardinal de
Je n'ai pas vraiment de solution générale, mais je te propose ceci :
Pour
3- Déduis-en alors le cardinal de
par jlb » 15 Déc 2013, 16:37
capitaine nuggets a écrit:Ok, cherchons alors le cardinal de
Je n'ai pas vraiment de solution générale, mais je te propose ceci :
Pour.
1- Quel est le cardinal de?
2- Montre que l'applicationdéfinie par
3- Déduis-en alors le cardinal de
ça marche, donc le cas est réglé quand la somme vaut 6, cela me donne 5!/[(n-1)!(6-n)!] si je n'ai pas fait d'erreurs!
comment on trouve pour d'autres valeurs de la somme?
par capitaine nuggets » 15 Déc 2013, 20:40
capitaine nuggets a écrit:Je n'ai pas vraiment de solution générale, mais je te propose ceci (...)
Si tu regardes bien, j'ai trouvé une bijection d'un ensemble F dont on connais le cardinal.
Il faudrait donc faire la même chose pour n>6.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par jlb » 15 Déc 2013, 20:56
capitaine nuggets a écrit:Si tu regardes bien, j'ai trouvé une bijection d'un ensemble F dont on connais le cardinal.
Il faudrait donc faire la même chose pour n>6.
euh?, pour p>6 merci en tout cas pour ce début.
Je sèche pour p>6. Une piste, svp?
par jlb » 17 Déc 2013, 00:25
Bonsoir, savez - vous s'il y a une solution à mon problème ou si je dois me résoudre à un algorithme pour obtenir mon résultat? Merci.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :