Dénombrement

par **pingouin estropié** » 22 Oct 2011, 18:39

Bonjour à Tous,

L'énoncé de mon pb est le suivant : Sachant que pour monter un escalier de N marches, il est possible de sauter au plus une marche, combien existe-il de façons S de le monter ? En particulier, la tour Eiffel compte marches, combien existe-il de façon de la monter ?

Après réflexion j'ai trouver comme formule S = la somme pour i variant de 0 à la partie entière de N/2 du nombre de partie à i éléments dans un ensemble à N-i éléments.

Au départ, j'ai essayé de calculer la somme en fonction de N mais je n'y suis pas arrivé, ensuite je suis passé à la calculatrice et ai fait un programme sur celle-ci pour la Tour Eiffel, mais elle affiche " Overflow " -Trop grand donc ...

Enfin, je suis passé sur excel pour calculer la somme pour N=1710 mais rien à faire, cela m'affiche #NOMBRE! - Tjrs trop grand :)

Je suis à cours d'idées, je réfléchis donc sur le calcul de la somme en fonction de N. Auriez-vous qqch à proposé ?

par **Skullkid** » 22 Oct 2011, 18:48

Bonjour, comment es-tu arrivé à ta formule pour S ?

par **SaintAmand** » 22 Oct 2011, 18:50

Bonsoir,

pingouin estropié a écrit:L'énoncé de mon pb est le suivant : Sachant que pour monter un escalier de N marches, il est possible de sauter au plus une marche, combien existe-il de façons S de le monter ? En particulier, la tour Eiffel compte marches, combien existe-il de façon de la monter ?

Note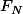

le nombre de façon de monter un escalier de N marches. Essaye d'établir une relation de récurrence entre les termes de la suite. As-tu calculé les premiers termes ?

par **Dlzlogic** » 22 Oct 2011, 18:54

Bonsoir,
Pour le nombre de marches de la tour Eiffel, ça ne m'étonne pas tellement (pas du tout).
Pour avoir un ordre d'idée, chaque groupe de 2 marches successives peut être franchi en une fois, ou en deux fois.
Donc, le solution est forcément de la forme 2^N, si N est le nombre de marches.
Souvenez-vous de l'architecte égyptien que acceptait de construire un temple avec les colonnes disposées d'une certaine façon, si on le payait de la manière suivante : sur un jeu d'échec, on pose un grain de blé sur la première case, deux sur la deuxième, 4 sur la troisième, 8 sur la quatrième et ainsi de suite, en doublant chaque fois jusqu'à la 64ème. Décomptes faits, le pharaon a renoncé.

Par contre, vous pouvez essayer de l'exprimer de façon approximative, avec des puissances de 10.

par **Skullkid** » 22 Oct 2011, 19:00

Dlzlogic a écrit:Donc, le solution est forcément de la forme 2^N, si N est le nombre de marches.

Ça veut dire quoi "de la forme 2^N" ? Il y a en effet des puissances de N qui apparaissent dans l'expression, mais ils ne sont pas exposant de 2...

SaintAmand a donné la piste pour trouver la valeur en fonction de N (et la notation F n'est pas anodine), mais je suis quand même curieux de savoir comment pingouin estropié a obtenu son expression, qui m'a l'air correcte.

par **pingouin estropié** » 22 Oct 2011, 19:40

J'y ai réffléchi assez longtemps :

Soit N un entier naturel. Soit k un élément de {0,1,...,partie entière de N/2}
Si on décide de sauter k marches, il y a (N-k,k) façons de les répartir sur le trajet (c'est le nombre de façon de choisir k billes parmis N-k)

Désolé si je m'exprime mal, j'ai fait un dessin pour trouver ça...

par **pingouin estropié** » 22 Oct 2011, 19:47

Pourquoi pas trouver une relation de récurrence comme vous me le conseiller Saint-Amant, et ensuite programmer la suite sur ma calto mais elle me dira encore "overflow" j'imagine

par **SaintAmand** » 22 Oct 2011, 20:12

pingouin estropié a écrit:Pourquoi pas trouver une relation de récurrence comme vous me le conseiller Saint-Amant, et ensuite programmer la suite sur ma calto mais elle me dira encore "overflow" j'imagine

Quelque soit la méthode utilisée, le résultat finale fera 279 chiffres.

Il se trouve qu'il est très simple d'établir une relation de récurrence. À partir de cette relation de recurrence il est possible d'obtenir une formule explicite moyennant le recours à un peu d'algèbre linéaire.

Indication: tu veux gravir n marches. Combien de façons différentes se terminent par un saut de 1 marche ? et par un saut de 2 marches ?

Pour le résultat exact tu peux écrire un script de quelques lignes en langage Python.

par **Skullkid** » 22 Oct 2011, 20:23

SaintAmand a écrit:Quelque soit la méthode utilisée, le résultat finale fera 279 chiffres.

T'es sûr ? J'obtiens 358 chiffres de mon côté...

De toute façon, je ne pense pas qu'on te demande l'écriture décimale de S pour N = 1710, puisqu'il est possible d'en donner une formule exacte compacte. Cette formule exacte te donnera l'ordre de grandeur quand tu l'entreras sur une calculatrice ou logiciel de calcul.

par **SaintAmand** » 22 Oct 2011, 20:32

Skullkid a écrit:T'es sûr ? J'obtiens 358 chiffres de mon côté...

Tu as raison.

par **Skullkid** » 22 Oct 2011, 20:36

Ok, merci, je cherchais en vain où je pouvais m'être gourré...

Dénombrement

Dénombrement

Qui est en ligne