Dénombrement probabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 30 Mai 2022, 18:33
par Cezoro » 30 Mai 2022, 18:33
Bonjour,
j'ai besoin d'aide sur l'égalité suivante:
avec A variable aléatoire suivant la loi uniforme sur l'ensemble des parties à m éléments de [1,...,n]
m<n
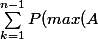\leq k)}=(\sum_{k=m}^{n-1}{\bigl(\begin{smallmatrix}<br />k\\m <br /><br />\end{smallmatrix}\bigr)})/\bigl(\begin{smallmatrix}<br />n\\m <br /><br />\end{smallmatrix}\bigr))
ni l'égalité suivante
}=\bigl(\begin{smallmatrix}<br />n\\m+1 <br /><br />\end{smallmatrix}\bigr))
qui "représente le nombre de façons de choisir m+1 éléments parmi n en fonction de leur maximum"
Je ne comprends pas cette phrase ni sa traduction en équation mathématique.
Bonne soirée
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Mai 2022, 09:35
par GaBuZoMeu » 31 Mai 2022, 09:35
Bonjour,
Une partie à
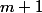
éléments de
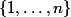
dont le maximum est
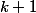
, c'est la réunion de

et d'une partie à

éléments de

.
Est-ce que tu comprends ça ?
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 31 Mai 2022, 10:39
par Cezoro » 31 Mai 2022, 10:39
Oui je comprends cela.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Mai 2022, 11:58
par GaBuZoMeu » 31 Mai 2022, 11:58
Bon, ben tu devrais comprendre alors la deuxième égalité.
Pour la première, est-ce que tu comprends que l'évènement
\leq k)
équivaut à l'évènement

?
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 31 Mai 2022, 12:34
par Cezoro » 31 Mai 2022, 12:34
D'accord j'ai compris la deuxième égalité,
Choisir m+1 parmi n, cela revient au nombre de façons (d'où la somme) de choisir m éléments parmi [1 ,...,k] avec k+1 maximum, pour tous les maximums possibles(>=m).
Au sujet de la première égalité, oui je comprends cela. Mais l'égalité est encore floue pour moi.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Mai 2022, 13:03
par GaBuZoMeu » 31 Mai 2022, 13:03
Continue à réfléchir.
Au passage, tu peux remarquer que l'événement
\leq k)
est vide si
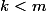
.
-
Cezoro
- Messages: 7
- Enregistré le: 30 Mai 2022, 18:19
-
 par Cezoro » 31 Mai 2022, 13:55
par Cezoro » 31 Mai 2022, 13:55
Oui effectivement le résultat découle clairement de P(A inclus dans [1,....,k])=(m parmi k)
Merci pour l'aide apportée.
Bonne journée
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Mai 2022, 16:06
par GaBuZoMeu » 31 Mai 2022, 16:06
Cezoro a écrit:Oui effectivement le résultat découle clairement de P(A inclus dans [1,....,k])=(m parmi k)
Hum... Une probabilité plus grande que 1 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
