Dénombrement: nombre de boucle.

[Pierebean]

Bonjour à tous,

Je suis nouveau sur ce forum j'espère que je respecter les rêgles(en fait je ne sais pas si je suis dans la bonne section).

Voici mon problème:

Vous avez n personnes. Dans un panier (c'est plus champêtre que l'urne de nos livres de maths) se trouvent les noms de chacune de ces n personnes.

Chaque personne tire au hasard le nom d'un autre personne. Il ne peut pas se choisir lui même.

Ma question est la suivante:
Quelle est le nombre le plus probable de boucle pour n personnes.

J'appele boucle la situation suivante:

Michel tire le nom "Jacques".
Jacques tombe sur "Hubert".
Hubert tombe sur "Jennifer".
Jennifer tombe sur Michel.
La boucle est bouclée.


J'ai fait une essai avec ma famille. Nous étions 31 nous sommes tombé sur quatres boucles.



En gros, voilà ce que je cherche. Je ne vois vraiment pas comment résoudre ce problème d'une manière théorique. j'imagine qu'il faut utiliser les combinaisons.
Je me suis dis que je pouvais résoudre l'affaire en utilisant le c en programmant un grand nombre de tirage. Le problème c'est que je ne vois pas comment programmer la notion de boucle.

Merci de votre aide.
A vous lire.

Pierebean

[Flodelarab]

c loin d'etre une question de supérieur. On fait ça au lycée.

on tire n personnes parmi n en tenant compte de l'ordre et sans répétition.
On a donc un arrangement de n parmi n
soit n! possibilité.

bien plus que 4 :-)

ok ?

[emdro]

c loin d'etre une question de supérieur. On fait ça au lycée.

on tire n personnes parmi n en tenant compte de l'ordre et sans répétition.
On a donc un arrangement de n parmi n
soit n! possibilité.

bien plus que 4

ok ?

Cela ne répond pas à la question de savoir le nombre de BOUCLES le plus probable...

[nuage]

Salut,
je ne suis pas d'accord avec Flodelarab qui, je pense, n'a pas vaiment compris la question.

De fait la question me semble très difficile. Le proplème est de calculer le nombre moyen de cycle dans les éléments de Sn.
Et je connais mal le sujet.
Je vais essayer d'y réfléchir, mais sans promesse de réponse.

A+

[Flodelarab]

j'ai négligé l'identité du tireur ...

Mais a part ça.

Qu'est ce qui te gene dans ma réponse Nuage ?

[nuage]

@ Flodelarab : la question est de trouver, non le nombre de permutations (sans point fixe ce qui rend déja le problème assez dur) mais de trouver le nombre de "boucles" (le terme consacré est cycle)
Pour donner un exemple élémentaire :
Avec 4 personnes il y a 24 permutations possibles. Parmi elles 6 sont sans points fixes (1;2)(3;4) , (1;3)(2;4) , (1;4)(2;3) et les 3 permutations circulaires.
Soit en moyenne 1,5 cycle et équiprobabilté entre 1 et 2 cycle

A+

Modification : il y a une (des) faute grossière ci dessus. On ne devrait jammais répondre trop vite.
Toutes mes excuses

[emdro]

Pourrait-on compter le nombre de façons de fabriquer:

1 cycle: (n-1)! -en décidant de fixer le premier personnage, il y a n-1 choix pour son tirage, n-2 pour le deuxième, sinon, le cycle s'arrêterait, ...-

2 cycles: longueurs respectives k et n-k : [C(n,k)*(k-1)!]*[C(n-k,n-k)*(n-k-1)!] Il faut ensuite additionner pour tous les k entre 2 et (n-k)/2 (distinguer selon que n est pair ou impair)

3 cycles: longueurs respectives k, l, et n-(k+l),
il faut fixer k<=l<=n-(k+l), Il y a [C(n,k)*(k-1)!]*[C(n-k,l)*(l-1)!]*[1*(n-k-l)!] possibilités différentes. Ensuite, il faut veiller à ne pas compter plusieurs fois les permutations avec deux ou trois cycles de même longueur (k=l par exemple)

etc?

Cela vous semble correct dans le raisonnement? Et généralisable?

[Flodelarab]

OK!

Effectivement, j'avais pas compris le 4.

[nuage]

Salut,
C'est certainement une bonne piste.
Et ça prouve que l'exemple que j'ai donné plus haut est faux.

[Flodelarab]

Pierebean, tu parlais de programmation... Voici un bon exemple de récursivité.


A chaque fois tu considères que l'utilisateur choisit entre :
Le premier maillon.
Un nouveau maillon.
Puis tu passes au mayon suivant si tu as pas bouclé.
Si tu as bouclé, tu recommences à 0 avec le groupe restant

Dans tous les cas tu te méfieras de savoir si le tireur est dans le groupe restant.

[yos]

Bonsoir.
Est-ce que deux personnes différentes peuvent tirer le même nom? J'imagine que non.
Le fait d'interdire les points fixes à la permutation fait qu'on raisonne, non pas sur n! permutations mais sur n!/e dérangements (l'entier le plus proche de n!/e en fait, mais n!/e est pratiquement un entier). Je dirais que cela complique les choses et j'ai envie d'autoriser les cycles de longueur 1 (cas où on tire son propre nom). Désolé de changer ton exercice.
Dans ces conditions, il y a le résultat suivant :
"le nombre de permutations de {1,...,n} qui se décomposent en exactement k cycles est égal au coefficient de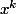 du polynôme . "

[emdro]

Pierebean, tu parlais de programmation... Voici un bon exemple de récursivité.


A chaque fois tu considères que l'utilisateur choisit entre :
Le premier maillon.
Un nouveau maillon.
Puis tu passes au mayon suivant si tu as pas bouclé.
Si tu as bouclé, tu recommences à 0 avec le groupe restant

Dans tous les cas tu te méfieras de savoir si le tireur est dans le groupe restant.

??????????????

[nuage]

Bravo Yos :++: :++: :++:

[yos]

Ben j'ai pas résolu l'exercice, j'ai changé l'énoncé pour parvenir à le faire.

[emdro]

Ce n'est pas simple maintenant, de retirer les permutations comportant des cycles de longueur 1?

[yos]

Ce n'est pas simple maintenant, de retirer les permutations comportant des cycles de longueur 1?

A cette heure-ci, c'est pas évident.
D'ailleurs je ne vois pas le plus gros coef de mon polynôme (c'est la question initiale). Celui de x²? Du terme du milieu?
Bon à demain.