Bonjour,
Je suis amateur de maths et de jeux de société.
Si je lance 10 fois un dé à 20 faces, quelles sont mes chances de tomber au moins 4 fois sur la même face ?
Existe-t-il une formule pour le cas général ? C'est à dire :
Si je lance n fois un dé à p faces, quelles sont mes chances de tomber au moins k fois sur la même face ?
Je n'arrive pas à trouver sur internet, mais il faut dire aussi que je ne sais pas trop quoi taper dans le moteur de recherche.
Merci de votre aide.
Dénombrement appliqué aux jeux de société
6 messages
- Page 1 sur 1
Re: Dénombrement appliqué aux jeux de société
Loi binomiale
ou encore loi normale, si tu veux traiter des cas avec 30 lancers ou plus .
La loi normale est plus simple à calculer, elle donne une approximation largement suffisante dès qu'on a un nombre important de lancer.
Il y a quelques années, on mettait le seuil à 30 lancers. Aujourd'hui, les moyens informatiques ont changé, et on sait calculer des lois binomiales pour 30 , 40, ou même 50 lancers... et donc on utilise de moins en moins la loi normale, on ne s'en sert que pour des nombres de lancers très élevés.
Connaître la loi binomiale, c'est le minimum syndical quand on dit qu'on est amateur de maths et de jeu de sociétés, et qu'on poste dans la rubrique 'supérieur'. C'est vraiment le strict minimum.
Pour ta 1ère question, même en connaissant parfaitement la loi binomiale, ça reste un exercice compliqué.
Commence par des questions un peu plus simples :
- probabilité d'avoir aucune fois la face n°1 quand on lance 10 fois un dé à 20 faces.
- probabilité d'avoir une fois et une seule la face n°1 quand on lance 10 fois un dé à 20 faces.
- probabilité d'avoir exactement k fois la face n°1 quand on lance 10 fois un dé à 20 faces.
Après, en faisant quelques impasses tout à fait acceptables, tu auras la réponse à ta question.
ou encore loi normale, si tu veux traiter des cas avec 30 lancers ou plus .
La loi normale est plus simple à calculer, elle donne une approximation largement suffisante dès qu'on a un nombre important de lancer.
Il y a quelques années, on mettait le seuil à 30 lancers. Aujourd'hui, les moyens informatiques ont changé, et on sait calculer des lois binomiales pour 30 , 40, ou même 50 lancers... et donc on utilise de moins en moins la loi normale, on ne s'en sert que pour des nombres de lancers très élevés.
Connaître la loi binomiale, c'est le minimum syndical quand on dit qu'on est amateur de maths et de jeu de sociétés, et qu'on poste dans la rubrique 'supérieur'. C'est vraiment le strict minimum.
Pour ta 1ère question, même en connaissant parfaitement la loi binomiale, ça reste un exercice compliqué.
Commence par des questions un peu plus simples :
- probabilité d'avoir aucune fois la face n°1 quand on lance 10 fois un dé à 20 faces.
- probabilité d'avoir une fois et une seule la face n°1 quand on lance 10 fois un dé à 20 faces.
- probabilité d'avoir exactement k fois la face n°1 quand on lance 10 fois un dé à 20 faces.
Après, en faisant quelques impasses tout à fait acceptables, tu auras la réponse à ta question.
Re: Dénombrement appliqué aux jeux de société
En fait suivant quelle est ta question la réponse de lycéen n'est peut-être pas tout à fait adapté.
Si tu fais 10 tirages (indépendants) de ton D20 (supposé équilibré) et que tu t'intéresse au nombre de 1 que tu as obtenu alors c'est bien la loi Binomiale qui t'intéresse (voir par exemple :https://fr.wikipedia.org/wiki/Loi_binomiale ).
Pour répondre à la question "quelle est la probabilité d'obtenir 4 fois 1 sur 10 lancer" il te faut bien utiliser directement la loi binomiale.
Pour répondre à la question "quelle est la probabilité d'obtenir au moins 4 fois 1 sur 10 lancer" tu peux utiliser la loi binomiale (en faisant la somme pour 4,5,....,20) ou approximer la loi Binomiale par la loi normale pour obtenir "plus rapidement" une valeur approximée. Avec excel ou python il vaut mieux faire le calcul exact...
Pour répondre à la question "quelle est la probabilité d'avoir au moins 4 fois la même face" sans préciser de quelle face il s'agit c'est plus délicat...
Donc quelle est ta question exactement : avoir au moins 4 fois 1, ou au moins 4 fois la même face ?
Si tu fais 10 tirages (indépendants) de ton D20 (supposé équilibré) et que tu t'intéresse au nombre de 1 que tu as obtenu alors c'est bien la loi Binomiale qui t'intéresse (voir par exemple :https://fr.wikipedia.org/wiki/Loi_binomiale ).
Pour répondre à la question "quelle est la probabilité d'obtenir 4 fois 1 sur 10 lancer" il te faut bien utiliser directement la loi binomiale.
Pour répondre à la question "quelle est la probabilité d'obtenir au moins 4 fois 1 sur 10 lancer" tu peux utiliser la loi binomiale (en faisant la somme pour 4,5,....,20) ou approximer la loi Binomiale par la loi normale pour obtenir "plus rapidement" une valeur approximée. Avec excel ou python il vaut mieux faire le calcul exact...
Pour répondre à la question "quelle est la probabilité d'avoir au moins 4 fois la même face" sans préciser de quelle face il s'agit c'est plus délicat...
Donc quelle est ta question exactement : avoir au moins 4 fois 1, ou au moins 4 fois la même face ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Dénombrement appliqué aux jeux de société
On est dans le domaine du 'réel'.
Si la vraie réponse à la question est 2.03% et qu'on donne comme réponse 2%, c'est largement suffisant.
Quand on a la probabilité d'avoir la face 1 au moins 4 fois, on multiplie par 20 et ça nous donne (environ) la probabilité d'avoir une face quelconque au moins 4 fois.
Pourquoi environ ? Parce que les configurations du type "4 fois la face 1 et 4 fois la face 2 et 2 autres faces quelconques " seront comptées 2 fois dans ce calcul.
On peut calculer la probabilité de ces cas là, mais ça doit être de l'orde de 10^-10 au mieux. Donc on peut faire l'impasse.
Dans un exercice de maths, il ne faudrait pas faire l'impasse. Ou il faudrait justifier cette impasse.
Mais de toutes façons, Umbre373 ne reviendra pas ... sauf pour me contredire.
Si la vraie réponse à la question est 2.03% et qu'on donne comme réponse 2%, c'est largement suffisant.
Quand on a la probabilité d'avoir la face 1 au moins 4 fois, on multiplie par 20 et ça nous donne (environ) la probabilité d'avoir une face quelconque au moins 4 fois.
Pourquoi environ ? Parce que les configurations du type "4 fois la face 1 et 4 fois la face 2 et 2 autres faces quelconques " seront comptées 2 fois dans ce calcul.
On peut calculer la probabilité de ces cas là, mais ça doit être de l'orde de 10^-10 au mieux. Donc on peut faire l'impasse.
Dans un exercice de maths, il ne faudrait pas faire l'impasse. Ou il faudrait justifier cette impasse.
Mais de toutes façons, Umbre373 ne reviendra pas ... sauf pour me contredire.
Re: Dénombrement appliqué aux jeux de société
Si si je reviens, merci beaucoup pour vos réponses.
Dans ma question, il s'agissait bien d'une face quelconque, et non une en particulier. Je suis d'accord pour dire que les tirages où on trouve plusieurs fois 4 faces identiques doivent être rares et ne changent pas grand chose au résultat.
Pour mon exemple concret, si j'ai bien compris ce que vous disiez, je pense que le plus simple est peut- être de faire 20*(1 - (la somme des chances d'obtenir exactement 0 fois, 1 fois , 2 fois ou 3 fois la face 1)).
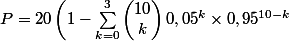)
Je voulais surtout savoir s'il existait une formule plus simple pour le cas générale. Afin de pouvoir évaluer différentes situations facilement, si je change le nombre de faces, de dés, ou de résultats identiques attendus. Mais visiblement changer une de ces variables implique à chaque fois de tout refaire avec plusieurs utilisations de la loi binomiale, si j'ai bien compris, on ne peut pas y couper.
Ma formule générale ressemblerait donc à cela (si je ne me suis pas mélangé les pinceaux):
Avec
n, le nombre de lancers
p, le nombre de faces du dé (supposé équilibré)
q, le nombre minimum de faces identiques attendues
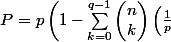^{k}\left(\frac{p-1}{p} \right)^{n-k}}\right))
J'espère vous avoir bien compris.
Encore merci
Dans ma question, il s'agissait bien d'une face quelconque, et non une en particulier. Je suis d'accord pour dire que les tirages où on trouve plusieurs fois 4 faces identiques doivent être rares et ne changent pas grand chose au résultat.
Pour mon exemple concret, si j'ai bien compris ce que vous disiez, je pense que le plus simple est peut- être de faire 20*(1 - (la somme des chances d'obtenir exactement 0 fois, 1 fois , 2 fois ou 3 fois la face 1)).
Je voulais surtout savoir s'il existait une formule plus simple pour le cas générale. Afin de pouvoir évaluer différentes situations facilement, si je change le nombre de faces, de dés, ou de résultats identiques attendus. Mais visiblement changer une de ces variables implique à chaque fois de tout refaire avec plusieurs utilisations de la loi binomiale, si j'ai bien compris, on ne peut pas y couper.
Ma formule générale ressemblerait donc à cela (si je ne me suis pas mélangé les pinceaux):
Avec
n, le nombre de lancers
p, le nombre de faces du dé (supposé équilibré)
q, le nombre minimum de faces identiques attendues
J'espère vous avoir bien compris.
Encore merci
Re: Dénombrement appliqué aux jeux de société
Tu peux faire quelques vérifications de cohérence.
- En prenant des valeurs un peu extrèmes, est-ce que cette formule donne toujours une probabilité entre 0 et 1.
En fait peut-être pas , parce qu'on sait qu'on a fait une impasse, et que cette formule n'est valable que si q n'est pas trop petit. Donc il faut tester des cas extrèmes, mais avec q petit.
- En calculant avec cette formule (n=10, p=20, q=4), c'est à dire l'énoncé de départ, tu trouves combien ?
- puis tu calcules (n=10, p=21, q=4) ... a priori tu sais anticiper, tu sais que le résultat doit être plus petit ( ou plus grand, j'ai la flemme de me concentrer...) . Est-ce que le résultat est conforme à la prévision.
- Idem avec 9 lancers au lieu de 10
Si les résultats ne sont pas conformes aux prévisions, la formule est fausse. S'ils sont conformes, alors c'est probablement bon.
- En prenant des valeurs un peu extrèmes, est-ce que cette formule donne toujours une probabilité entre 0 et 1.
En fait peut-être pas , parce qu'on sait qu'on a fait une impasse, et que cette formule n'est valable que si q n'est pas trop petit. Donc il faut tester des cas extrèmes, mais avec q petit.
- En calculant avec cette formule (n=10, p=20, q=4), c'est à dire l'énoncé de départ, tu trouves combien ?
- puis tu calcules (n=10, p=21, q=4) ... a priori tu sais anticiper, tu sais que le résultat doit être plus petit ( ou plus grand, j'ai la flemme de me concentrer...) . Est-ce que le résultat est conforme à la prévision.
- Idem avec 9 lancers au lieu de 10
Si les résultats ne sont pas conformes aux prévisions, la formule est fausse. S'ils sont conformes, alors c'est probablement bon.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
