Demostration du théoreme de diagonalisation

[ousintkd]

Salut tout le monde!

Je voudrais de l'aide pour démontrer le théorème suivant:

Soit A un matrice carrée d'ordre n d'élément d'un ensemble K, Pa son polynôme caractéristique. on suppose qu'il existe y1, y2,..., yn appartenant à K et a1, a2, ..., ar appartenant à l'ensemble des entier naturel privé de 0 tels que:
quelque soi t appartenant à K,

Pa(t) = (y1-t)^a1 * (y2 - t)^a2 * ... * (yn - t)^ar

Alors A est diagonalisable si et seulement si quelque soi i appartenant à {1, ..., r} : dim(A-yi In) = ai

avec In la matrice unité d'ordre n. Merci

[tize]

Petit problème, avec tes notations la matrice ne peut être d'ordre n : c'est yr et pas yn...et c'est dim(Ker(A-yi In)) = ai.
Premièrement il faut montrer que les espaces propres sont en sommes directs. Ensuite montrer que . La suite est assez simple, il me semble...

[ousintkd]

Merci!

Tu raison à propos des erreurs de notation, ca te derrangerais de faire cette demostration?

[tize]

Je peux essayer mais je ne suis pas sûr que cela t'apporte beaucoup par rapport aux démonstration que tu peux trouver dans n'importe quel livre d'algèbre matricielle, tu auras avec moi au mieux la rigueur en moins au pire une erreur dans la démo :

Soit f l'endomorphisme associé à A.
Premièrement démontrons que les sont en sommes directs:
Par récurrence, si il y en a 1 seul c'est évident, on suppose que c'est vrai pour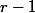 espaces propres alors soit des espaces propres ( pour 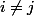). Soient et 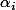des éléments de corps tels que supposons que l'un des 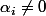(par exemple ) on a alors

et d'une part et d'autre part
Donc et d'après l'H.R. (et comme les ) on en déduit pour tout i.

Deuxièmement on montre que :
Remarquons tout d'abord que tout espace propre est stable par f. On en déduit (mais c'est à démontrer) que (le polynôme caractéristique de la réduction de f à ) divise . Or et comme nécessairement ........Reste à exprimer A dans une base de vecteurs propres.

[ousintkd]

Soient

c'est pas ?

[ousintkd]

Soient

c'est pas -{} ?

[tize]

Oui c'est ça :we: