Bonjour,
J'ai besoin d'un peu d'aide pour démontrer les surjections.
Est ce que je dois trouver un seul point qui a un antécédent.
par exemple pour démontrer que sin(x) est surjective sur R est ce qu'il est possible de faire comme ça?
0=sin(0) alors 0 admet un antécédent d'où sin(x) est surjective.
ou il faut démontrer que pour tout y de [-1,1] il existe x tel que y=f(x)
merci
Demontrer une surjection.
4 messages
- Page 1 sur 1
les surjections
random a écrit:il faut démontrer que pour tout y de [-1,1] il existe x tel que y=f(x)
:++:
oui, c'est cela. Il faut montrer que tout élément du codomaine de la fonction (ensemble d'arrivée) est une image. Voilà quelques résultats sur les surjections:
A)
- la composée de deux surjections est une surjection
B)
- l'image d'un intervalle I par une fonction continue f est un intervalle J
La restriction de f au codomaine J est surjective.
C)
une application f , d'un ensemble E vers F, se décompose ainsi:
c'est la décomposition canonique d'une application en le produit d'une surjection, d'une bijection et d'une injection.
D)
f est surjective ssi f admet un inverse g à droite pour la composition des applications.
Pour chaque y de l'ensemble f(E), g(y) est définie en choisissant (axiome du choix) un élément x dans l'image réciproque
Pour les y dans
pour un
par ex, la fonction "carré" , de
et évidemment, considérer une racine carrée, c'est choisir une inverse plutôt
que l'autre, ce qui fait...bien flipper les élèves de Seconde. :zen:
E)
Soient E et F deux ensembles. on prend comme définition de
il existe une surjection
F) une surjection classique est celle donnée par une relation d'équivalence:
qui, à un élément, associe sa classe.
mathelot a écrit::++:
oui, c'est cela. Il faut montrer que tout élément du codomaine de la fonction (ensemble d'arrivée) est une image. Voilà quelques résultats sur les surjections:
A)
- la composée de deux surjections est une surjection
B)
- l'image d'un intervalle I par une fonction continue f est un intervalle J
La restriction de f au codomaine J est surjective.
C)
une application f , d'un ensemble E vers F, se décompose ainsi:ssi
est une relation d'équivalence.
(surjection)
(bijection)
(injection)
c'est la décomposition canonique d'une application en le produit d'une surjection, d'une bijection et d'une injection.
D)
f est surjective ssi f admet un inverse g à droite pour la composition des applications.
Pour chaque y de l'ensemble f(E), g(y) est définie en choisissant (axiome du choix) un élément x dans l'image réciproque.
Pour les y dans\
, on fixe
pour unarbitraire.
par ex, la fonction "carré" , desur
a deux inverses à droite:
et
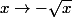
et évidemment, considérer une racine carrée, c'est choisir une inverse plutôt
que l'autre, ce qui fait...bien flipper les élèves de Seconde. :zen:
E)
Soient E et F deux ensembles. on prend comme définition dela propriété:
il existe une surjection
F) une surjection classique est celle donnée par une relation d'équivalence:
qui, à un élément, associe sa classe.
merci beacuop mathelot
j'ai compris
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
