Démontrer qu'une proposition est fausse

[L1M12014]

Bonjour, je suis en L1 Mass et il y a une question d'un exercice que je n'arrive pas à résoudre.

Montrer que pour tout x appartenant à ]2, +infini[, p(x) est fausse.
Sachant que P(x) est : "Pour tout e>0, x-2
Merci de bien vouloir m'aider.

[DivaythFyr]

Bonjour,

implique une preuve par contre-exemple.

[beagle]

Bonjour,

implique une preuve par contre-exemple.

Ben pas dans cet exo, on veut que p(x) soit tout le temps faux,
ce qui est bien le cas si x pris au-delà de 2,
il ne peut pas ètre plus petit que 2 + e

[Ben314]

Salut,
A mon avis, ce qui est attendu par celui qui a posé l'exercice, c'est que tu écrive la négation de P(x) puis que tu démontre que cette négation est vraie pour tout réel x>2.

[L1M12014]

Voici l'énoncé complet :

Pour x un nombre réel, on considère la proposition :
P(x) : "Pour tout e>0, x-21) Soit x appartient a R. Que signifie "P(x) est fausse" ?
2) Est-ce que P(1) est vrai ? P(3) ? P(2) ? P(2,1) ? P(2,01) ?
3) Montrer que pour tout x appartient ]2 ; +infini[, P(x) est fausse.

J'ai répondu aux questions 1 et 2. Je veux juste que vous m'expliquiez comment faire pour la question 3 ? Je suis tenté de faire un raisonnement par l'absurde non ?

[mathelot]

Bonsoir,

un nombre réel peut être défini par la coupure (A,B) , A, B étant deux ensembles de rationnels adjacents

ex



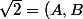(on ne pose pas le problème de la borne commune à A et B)

donc

pour

[chan79]

[quote="L1M12014"]Voici l'énoncé complet :

Pour x un nombre réel, on considère la proposition :
P(x) : "Pour tout e>0, x-22
soit e=(x-2)/2
on a x-2 >(x-2)/2 donc x-2>e
P(x) est donc fausse

[Doraki]

T'as répondu quoi à la question 2 ?