sticto a écrit:Ah pardon:
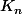
=
 dx)
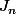
=
 dx)
Tu dois pouvoir écrire u(n-1)-un de façon a te ramener a ta question 1, ainsi avoir quelque chose de la forme :
u(n-1)-u(n) = f(n) J(2n), où tu auras donc déterminé f.
D'ailleurs j'ai comme l'impression qu'il y a une erreur de signe dans ta relation entre J et k Parce que J(2n) est positive, tout comme K(n) or du coup ton terme de droite est négatif ..
Par ailleurs J(2n) est calculable par récurrence.
dans l'integrale de J(2n), écris cos^(2n)(x) = cos(x)cos^(2n-1)(x) et intègre par parties pour retomber sur J(2n) et J(2(n-1)), tu obtiens une relation de récurrence que tu peux résoudre avec J0 = pi/2 (le pi apparaît !) et qui doit pas mal se simplifier avec le "f" trouvé avant pour ne te laisser que pi/(4n^2). (je n'ai pas été au bout du calcul mais ça part bien en tout cas)
Damien
=
=