Démonstrations congruences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Oct 2010, 18:30
par Dinozzo13 » 05 Oct 2010, 18:30
Bonsoir, y aurait-il un moyen original ou malin de démontrer que si
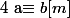
et
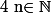
alors
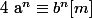
.
C'est-à-dire, sans passer par la récurrence ou la formule du binôme de Newton.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 18:40
par benekire2 » 05 Oct 2010, 18:40
Salut, a^n-b^n=(a-b)(...) mais le truc , c'est comment montrer cette égalité ? Y a quand même une récurrence derrière ..
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 05 Oct 2010, 19:16
par windows7 » 05 Oct 2010, 19:16
cette formule est generalement fausse ...
passons, la classe de x^n est ( la classe de x )^n
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 19:22
par benekire2 » 05 Oct 2010, 19:22
Quelle formule est fausse ??
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 05 Oct 2010, 19:25
par windows7 » 05 Oct 2010, 19:25
a^n-b^n= (a-b)( ..
c'est generalement faux !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 19:28
par Olympus » 05 Oct 2010, 19:28
windows7 a écrit:a^n-b^n= (a-b)( ..
c'est generalement faux !
"Généralement vrai" = "Vraie sur toute structure algèbrique" ? ^^
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 05 Oct 2010, 19:30
par windows7 » 05 Oct 2010, 19:30
c'est vrai dans tout algebre commutative de banach.
si c'etait vrai disons dans lanneau des matrice(n*n) ca se saurait !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 19:31
par Olympus » 05 Oct 2010, 19:31
Je savais à quoi m'attendre :ptdr:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 05 Oct 2010, 19:35
par Nightmare » 05 Oct 2010, 19:35
windows7 > Une algèbre de Banach commutative? Pourquoi parler de norme? Cette égalité est bien vraie dans n'importe quel anneau commutatif, et plus généralement vraie dans un anneau quelconque dès que a et b commutent.
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 05 Oct 2010, 19:42
par windows7 » 05 Oct 2010, 19:42
Nightmare a écrit:windows7 > Une algèbre de Banach commutative? Pourquoi parler de norme? Cette égalité est bien vraie dans n'importe quel anneau commutatif, et plus généralement vraie dans un anneau quelconque dès que a et b commutent.
j'ai rarement eu loccasion de placer dans une frase " algebre commutative de banach ", jme suis di vu que c'est vrai c'est loccasion. :langue:
oui on est bien daccord un anneau commutatif suffit
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 19:44
par benekire2 » 05 Oct 2010, 19:44
Mais je vois pas où est le problème ? Ici Z/mZ est un anneau commutatif donc no problem.
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 05 Oct 2010, 19:46
par windows7 » 05 Oct 2010, 19:46
passons .. :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
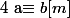 et
et 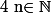 alors
alors 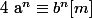 .
.