Démonstrations congruences
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Oct 2010, 18:19
par Dinozzo13 » 05 Oct 2010, 18:19
Bonsoir, y aurait-il un moyen original ou malin de démontrer que si
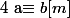
et
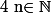
alors
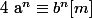
.
C'est-à-dire, sans passer par la récurrence ou la formule du binôme de Newton.
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 05 Oct 2010, 18:24
par Rebelle_ » 05 Oct 2010, 18:24
B'soir =)
Euh, je crois que par récurrence ça découle de ac congru à bd modulo n avec a, b, c et d dans Z ? :/
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Oct 2010, 18:29
par Dinozzo13 » 05 Oct 2010, 18:29
Encore une fois, je me suis trompé de rubrique, je vais donc rouvrir cette discussion dans le supérieur.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 18:29
par Olympus » 05 Oct 2010, 18:29
Salut !
Dinozzo13 a écrit:y aurait-il un moyen original ou malin de démontrer que si
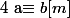
et
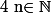
alors
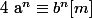
.
En remarquant par exemple que
\left( \bigsum_{k=0}^{n-1} a^k b^{n-k-1} \right) \equiv 0 \left[ m \right])
?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Oct 2010, 18:32
par Dinozzo13 » 05 Oct 2010, 18:32
nam, celle-là je l'ai trouvée :ptdr:
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 05 Oct 2010, 18:32
par Rebelle_ » 05 Oct 2010, 18:32
Ne serait-ce pas le binôme de Newton ? Je l'ai vu dans un exo, je crois, sans pour autant réussir à le manipuler... (a)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 05 Oct 2010, 18:32
par Joker62 » 05 Oct 2010, 18:32
Edit : bah grilled :o
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Oct 2010, 18:34
par Dinozzo13 » 05 Oct 2010, 18:34
Rebelle_ a écrit:Ne serait-ce pas le binôme de Newton ? Je l'ai vu dans un exo, je crois, sans pour autant réussir à le manipuler... (a)
Trouvé aussi, c'est pour ça que j'ai dit : "sans le binôme de Newton" ^^
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 05 Oct 2010, 18:37
par Rebelle_ » 05 Oct 2010, 18:37
Que penses-tu de ma solution ? C'est la démo de ma prof :P
PS : oh, un revenant ;D

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 18:40
par Olympus » 05 Oct 2010, 18:40
Rebelle_ a écrit:Que penses-tu de ma solution ? C'est la démo de ma prof

Dinozzo13 a écrit:sans passer par la récurrence
Sinon, je n'ai pas d'autre preuve "élégante" en tête ...
Je peux te dire que dans
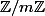
c'est trivial vu que
^n = \bar{x^n})
, mais c'est un peu une arnaque ^^
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 18:42
par benekire2 » 05 Oct 2010, 18:42
Le problème de la réécriture a^n-b^n=(a-b)(...) c'est qu'il y a quand même une idée de récurrence derrière ! Bon, j'ai répondu pareil sur l'autre topic, j'avais pas vu celui là ..
Et bonjour tout le monde !!
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 05 Oct 2010, 18:44
par Rebelle_ » 05 Oct 2010, 18:44
Oh Dinozzo tu as édité :P Au début tu avais juste mis sans binôme (que je ne connais pas donc ça va) ^^'
Eh bien je ne sais pas maintenant, je laisse la parole aux experts !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 18:44
par Olympus » 05 Oct 2010, 18:44
Pas besoin de récurrence pour ta formule benekire, il suffit de développer et de voir les termes s'annuler entre eux ;-)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 18:49
par benekire2 » 05 Oct 2010, 18:49
Ben oui, olympus je sais je sais :zen: mais ça ne me parrait pas hyper propre ...

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 05 Oct 2010, 19:18
par Olympus » 05 Oct 2010, 19:18
benekire2 a écrit:Ben oui, olympus je sais je sais :zen: mais ça ne me parrait pas hyper propre ...
\left( \bigsum_{k=0}^{n-1}a^k b^{n-k-1} \right) &=& \bigsum_{k=0}^{n-1}a^{k+1} b^{n-k-1} - \bigsum_{k=0}^{n-1} a^kb^{n-k}\\<br /> &=& a^n-b^n + \bigsum_{k=0}^{n-2}a^{k+1}b^{n-k-1} - \bigsum_{k=1}^{n-1} a^k b^{n-k} \\<br /> &=& a^n - b^n + \bigsum_{k=0}^{n-2} a^{k+1}b^{n-k-1} - \bigsum_{k=0}^{n-2} a^{k+1}b^{n-k-1} \\<br /> &=& a^n-b^n<br />\end{array})
Cela me parait propre moi :zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 05 Oct 2010, 19:24
par benekire2 » 05 Oct 2010, 19:24
Classiquement c'est comme ça que je fais pour montrer cette formule, mais je ne vois pas pourquoi je ne m'autorise pas à l'utiliser pour me passer de la récurrence.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
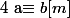 et
et 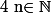 alors
alors 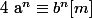 .
.