Démonstration D'une Propriété

[Georges10]

Bonjour à tous j'espère que vous allez bien. OK il y'a une propriété dont je ne comprend pas bien la démonstration. Je ne comprend pas comment passe-t-on de la 2 ème ligne à la 3 ème ligne.
Voici la démarche :
Merci d'avance !

[hdci]

Bonjour.
Dans la seconde ligne, il y a deux "sigmas". Chaque sigma est une somme.
Quand on multiplie deux facteurs qui sont constitués de sommes de termes, on peut développer, et on obtient une somme de multiplications des termes :

(a1+a2+a3)(b1+b2+b3)=a1b1+a1b2+a1b3+ (etc.)

Donc somme (ai) multiplié par somme(bj) est égal à somme des (aibj)

Ensuite, dans l'expression, quand on multiplie x puissance p par x puissance q, on obtient x puissance (p+q), et en appelant p+q=r, dans la troisième ligne on regroupe tous les termes en x puissance r (ce qui revient à additionner tous les facteurs correspondants).

Si tu veux comprendre plus en détail, fais le "en extension" avec des petites valeurs pour n et m (par exemple, n=2 et m=3).

[Georges10]

Merci pour ta reponse.

Donc somme (ai) multiplié par somme(bj) est égal à somme des (aibj) .

Oui mais qu′en est il des indices . Selon moi , on trouve ∑ᵢ₌₁ ₐ ₃ ( ∑ⱼ₌₁ ₐ ₃ ( aᵢbⱼ ) ) .[/quote]

quand on multiplie x puissance p par x puissance q, on obtient x puissance (p+q), et en appelant p+q=r.
.

J ′ai un problème avec la valeur de depart et de fin des indic

[hdci]

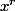
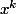
Le terme est obtenu par , puis , puis , etc., autrement dit avec venant du développement de (1+x)^n et venant du développement de

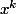
Or le coefficient binomial en facteur de est dans le développement de
Donc le coefficient qui multiplie est , autrement dit pour l'indice k on trouve dans le développement le terme suivant



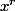
Donc pour r fixé, en mettant en facteur on trouve bien



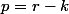
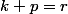
Maintenant si on appelle , la somme de k=0 à r est égale à la somme de ce qui fait qu'on a bien pour l'indice r le terme suivant



Il reste à déterminer l'ensemble des r possibles : or comporte tous les exposants de x compris entre 0 et n, et , entre 0 et m. Les exposants s'ajoutant quand on multiplie, cela fait dans le développements des exposants allant de 0+0 à m+n : ce sont donc bien les bornes de variations de r et on obtient ainsi

[hdci]

Remarque : je suis allé un peu vite dans ce qui précède, car dans il est possible, si , que .

En fait il aurait fallu écrire



Et en posant comme définition pour on obtient bien

[Georges10]

Merci beaucoup.