Démonstration d'un théorème de Poncelet
15 messages
- Page 1 sur 1
Démonstration d'un théorème de Poncelet
J'aurais besoin de la démonstration du théorème de Poncelet suivant:
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./p/poncelet.html
Pourriez-vos m'aider à la trouver s'il vous plait? Ou si vous avez une démo de ce th., pourriez-vous me la donner svp? C'est plutot urgent! Merci
http://www.bibmath.net/dico/index.php3?action=affiche&quoi=./p/poncelet.html
Pourriez-vos m'aider à la trouver s'il vous plait? Ou si vous avez une démo de ce th., pourriez-vous me la donner svp? C'est plutot urgent! Merci
C'est pour un TIPE ?
En fait la démonstration du théorème ne m'a pas l'air très compliquée, mais pour bien comprendre il faut quand même connaître de la géométrie projective, ce qui n'est pas du tout au programme en maths spé, si tu n'en as jamais fait ça risque d'être assez dur. C'est possible qu'il existe des démonstrations sans géométrie projective, mais je n'ai pas d'autres livres sous la main pour regarder, si tu vas dans une BU tu peux regarder s'il est dans les livres de Berger (Géométrie), ou Audin (Géométrie aussi), ou Ladegaillerie (Géométrie pour le CAPES et l'agrégation), ou d'autres livres de géométrie (Il y a d'autres théorèmes de Poncelet, qui parlent de tangentes et de bissectrices, il y a peut-être un lien avec ce théorème, même si je ne vois pas lequel là comme ça...). C'est normal que tu trouves des liens vers des bibliographies d'agrég, on ne fait quasiment plus de géométrie avant l'agrég ou le CAPES aujourd'hui, d'ailleurs tous les livres que j'ai cités sont des livres utilisés pour préparer l'agrégation ou le CAPES.
En fait Samuel montre que s'il existe un point et un entier
et un entier  tel que
tel que  , c'est vrai pour tout point (avec le même
, c'est vrai pour tout point (avec le même  ).
).
La démonstration se fait avec des correspondances (2,2) :
On appelle correspondance (2,2) de C dans C une courbe B de C×C définie par une équation polynomiale F(u,v) = 0, où F est de degré partiel égal à 2 en u et v. u et v désignent les abscisses projectives des points de C (... et de C) (une conique s'identifie à une droite projective).
Un point m de C est un point fixe de B si\in B) . Pour tout m il y a deux points de C en correspondance avec m, qui peuvent être confondus (ce sont les deux racines de F(m,v) = 0). Si m est racine double de l'équation en v F(m,v) = 0, ça fait 2 points fixes. Si B ne contient pas la diagonale I (u=v), elle a 4 points fixes, les racines de l'équation F(m,m) = 0.
. Pour tout m il y a deux points de C en correspondance avec m, qui peuvent être confondus (ce sont les deux racines de F(m,v) = 0). Si m est racine double de l'équation en v F(m,v) = 0, ça fait 2 points fixes. Si B ne contient pas la diagonale I (u=v), elle a 4 points fixes, les racines de l'équation F(m,m) = 0.
A tout point de C on fait correspondre les deux points
de C on fait correspondre les deux points 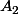 ,
,  tels que
tels que ) et
et ) soient tangentes à
soient tangentes à 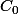 , en prenant les (autres) tangentes passant par
, en prenant les (autres) tangentes passant par 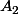 et
et  on obtient des points
on obtient des points 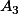 et
et  ... en recommençant on a des points
... en recommençant on a des points 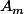 et
et  associées à
associées à  pour tout m, ça donne une correspondance
pour tout m, ça donne une correspondance 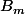 . La preuve consiste à montrer qu'avec l'hypothèse que pour un point, le polygone
. La preuve consiste à montrer qu'avec l'hypothèse que pour un point, le polygone ) « se referme » (
« se referme » (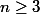 ),
), 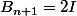 , I = identité (i.e. à tout point A de C,
, I = identité (i.e. à tout point A de C, 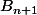 associe A et A). Pour cela on remarque que
associe A et A). Pour cela on remarque que 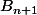 admet tous les
admet tous les  ,
, 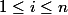 pour points fixes doubles, soit au moins
pour points fixes doubles, soit au moins  points fixes, donc elle contient I. On regarde de quoi se compose le reste de
points fixes, donc elle contient I. On regarde de quoi se compose le reste de 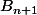 , et on montre que c'est encore
, et on montre que c'est encore  , en utilisant la classification des correspondances (2,2) qui est faite avant dans le chapitre (que j'ai pas lu en détail).
, en utilisant la classification des correspondances (2,2) qui est faite avant dans le chapitre (que j'ai pas lu en détail).
Rq : Samuel fait la démonstration pour des corps algébriquement clos (donc dans ici), mais si les ellipses C et
ici), mais si les ellipses C et 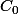 sont réelles on a bien le résultat dans
sont réelles on a bien le résultat dans  .
.
Il explique une autre démonstration avec des points critiques, mais elle ne m'a pas l'air plus simple (ni plus compliquée) que la première.
En fait la démonstration du théorème ne m'a pas l'air très compliquée, mais pour bien comprendre il faut quand même connaître de la géométrie projective, ce qui n'est pas du tout au programme en maths spé, si tu n'en as jamais fait ça risque d'être assez dur. C'est possible qu'il existe des démonstrations sans géométrie projective, mais je n'ai pas d'autres livres sous la main pour regarder, si tu vas dans une BU tu peux regarder s'il est dans les livres de Berger (Géométrie), ou Audin (Géométrie aussi), ou Ladegaillerie (Géométrie pour le CAPES et l'agrégation), ou d'autres livres de géométrie (Il y a d'autres théorèmes de Poncelet, qui parlent de tangentes et de bissectrices, il y a peut-être un lien avec ce théorème, même si je ne vois pas lequel là comme ça...). C'est normal que tu trouves des liens vers des bibliographies d'agrég, on ne fait quasiment plus de géométrie avant l'agrég ou le CAPES aujourd'hui, d'ailleurs tous les livres que j'ai cités sont des livres utilisés pour préparer l'agrégation ou le CAPES.
En fait Samuel montre que s'il existe un point
La démonstration se fait avec des correspondances (2,2) :
On appelle correspondance (2,2) de C dans C une courbe B de C×C définie par une équation polynomiale F(u,v) = 0, où F est de degré partiel égal à 2 en u et v. u et v désignent les abscisses projectives des points de C (... et de C) (une conique s'identifie à une droite projective).
Un point m de C est un point fixe de B si
A tout point
Rq : Samuel fait la démonstration pour des corps algébriquement clos (donc dans
Il explique une autre démonstration avec des points critiques, mais elle ne m'a pas l'air plus simple (ni plus compliquée) que la première.
En maths spé en ce moment c'est révisions d'oraux et fin (ou commencement) du TIPE, comme tu dis que c'est urgent et que ça m'étonnerait qu'on donne ça en exercice d'oral...
Admettre la démo, ça dépend de ce qu'il y a à côté dans ton TIPE, de l'importance du théorème pour leTIPE... Tu pourrais peut-être demander à ton prof de maths s'il n'y a pas de démonstration plus simple, et son avis pour admettre la démo ou non ?
Admettre la démo, ça dépend de ce qu'il y a à côté dans ton TIPE, de l'importance du théorème pour leTIPE... Tu pourrais peut-être demander à ton prof de maths s'il n'y a pas de démonstration plus simple, et son avis pour admettre la démo ou non ?
Rocklee a écrit: Au fait, quel est ton niveau?
Euh là je passe l'agrégation et je suis censée être en train de réviser pour les oraux.
J'ai aussi une autre question : comment tu fais pour taper les R ou C qui représentent les réels et les complexes??
Il faut utiliser la langage LaTeX, en écrivant les formules entre [ TEX] et [ /TEX] sans les espaces (il y a aussi le bouton TEX en haut quand on tape un message). Pour
Il y a un fil dessus ici (si tu fais une recherche tu en trouveras d'autres), et il y a un aide-mémoire pour les formules sur Wikipedia.
Après vérification, le théorème s'appelle « grand théorème de Poncelet », il y a deux autres théorèmes qui s'appellent premier et deuxième théorèmes de Poncelet et qui n'ont pas l'air d'avoir un rapport avec le grand théorème de Poncelet.
Il y a une démonstration du théorème dans le livre de Berger partie 16.6, je n'ai pas lu en détail, ce n'est pas la même que celle de Samuel mais elle n'a pas l'air plus simple.
Dans Méthodes modernes en géométrie de Fresnel il y a un exercice p.118 qui démontre le théorème de Poncelet dans le cas particulier n=3, je n'ai pas cherché donc je ne peux pas dire si c'est difficile...
Il y a une démonstration du théorème dans le livre de Berger partie 16.6, je n'ai pas lu en détail, ce n'est pas la même que celle de Samuel mais elle n'a pas l'air plus simple.
Dans Méthodes modernes en géométrie de Fresnel il y a un exercice p.118 qui démontre le théorème de Poncelet dans le cas particulier n=3, je n'ai pas cherché donc je ne peux pas dire si c'est difficile...
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
