Demonstration théorème Euler

[eduardo]

Bonjour à tous,

Je vous écris car j'éssaie de démontrer le théorème d'Euler qui dit :
Soit p un nombre premier, alors on a : avec le sombôle de Legendre.

Voici comment j'ai commencé :

Supposons que p et est premier et qu'il existe a tel que .
On a donc = 1 ou -1 :
J'ai réussi à montrer le premier cas ou = 1, par contre pour le second je n'arrive vraiment pas à trouver ce que cela induit sur ...

Merci d'avance pour votre aide :mur:

[L.A.]

Bonjour.

J'ai l'impression que tu pars un peu à l'aveuglette.
Tu peux essayer de suivre ce qui est ici par exemple :
http://perso.univ-lr.fr/gbailly/cours/chapt4.pdf

[eduardo]

Merci pour votre lien, je vais étudier ca et eventuellement revenir vers vous si j'en ai besoin.

[eduardo]

Et bien je n'ai pas bien avancé, a part que si a appartient a Z/nZ, alors la contradiction est directe. Mais dans le cas contraire, si a n'est pas un carré, je ne vois vraiment pas comment argumenter ?

Merci

[L.A.]

Donc, comme je disais, je ne pense pas qu'il faut un raisonnement par l'absurde à ce niveau.

Il faut supposer p impair (sans quoi la puissance (p-1)/2 n'a pas de sens), et on peut supposer p ne divise pas a (car dans ce cas les deux membres valent 0).

Posons q=(p-1)/2 et deux morphismes de groupes de (Z/pZ)* dans lui-même :

f : x -> x^2
g : x -> x^q

Tu peux vérifier que gof = fog = le morphisme trivial (x -> 1) (petit théorème de Fermat), puis que le noyau de f est {-1,1} et que l'image de g est aussi {-1,1} (le nombre de racines d'un polynôme dans un corps est plus petit que son degré). A partir de là, tu en déduis que

{carrés non nuls} = im f = ker g

[eduardo]

Jusqu'ici j'ai compris le raisonnement mais en quoi le fait que {carrés non nuls} = im f = ker g = {-1;1} permet il de conclure ?

Merci

[L.A.]

Très bien, alors tu sais que du coup

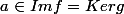
a est carré mod p ssi ssi a^q = 1 [p]
a n'est pas un carré mod p ssi a^q=-1 [p]

Donc tu retrouves bien ton symbole de Legendre.

Attention, c'est Im g et Ker f qui sont {-1,1}, pas Im f et Ker g, ceux-ci sont simplement égaux entre eux.