Demonstration

[kevin237]

justifier en moins de 5 lignes que l ensemble des bijections de E sur lui meme muni de la compisition des application est un groupe

[Ben314]

justifier en moins de 5 lignes que l ensemble des bijections muni de la compisition des application est un groupe

Fastoche (une ligne...) :
Ce n'est pas un groupe vu que l'on ne peut pas faire la composée VoU de deux bijections U et V lorsque l'ensemble d'arrivé de U est différent de l'ensemble de départ de V.

[kevin237]

on demande de justifier que c un groupe et en cours on justement donner ca comme exemple de groupe

[aymanemaysae]

Je crois que votre professeur vous a donné ça :

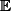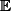Soit un ensemble non vide, et soit l'ensemble de toutes les bijections de dans 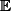. Le couple , où o est la composition des applications, est alors un groupe.

Votre question doit être reformulée pour préciser qu'il s'agit de l'ensemble des bijections de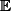 dans 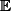, ce qui permettra à M.Ben314 de vous aider.

[Monsieur23]

justifier en moins de 5 lignes que l ensemble des bijections muni de la compisition des application est un groupe

Fastoche (une ligne...) :
Ce n'est pas un groupe vu que l'on ne peut pas faire la composée VoU de deux bijections U et V lorsque l'ensemble d'arrivé de U est différent de l'ensemble de départ de V.

D'un autre côté, est-ce que "l'ensemble des bijections" est un ensemble ? Chaque ensemble ayant sa bijection trivial, c'est a priori "plus gros" que la classe (propre) de tous les ensembles, non?

[Ben314]

Soit un ensemble non vide <- inutile , et soit l'ensemble de toutes les bijections de dans . Le couple , où o est la composition des applications, est alors un groupe.

D'un autre côté, est-ce que "l'ensemble des bijections" est un ensemble ? Chaque ensemble ayant sa bijection trivial, c'est a priori "plus gros" que la classe (propre) de tous les ensembles, non?

Tout à fait: ce n'est pas un ensemble.
Mais, pour montrer qu'il ne s'agissait pas d'un groupe, ça me semblait plus "élémentaire" d'évoquer qu'on ne peut pas composer les éléments plutôt que d'évoquer que ce n'est pas un ensemble.

[Monsieur23]

Mais, pour montrer qu'il ne s'agissait pas d'un groupe, ça me semblait plus "élémentaire" d'évoquer qu'on ne peut pas composer les éléments plutôt que d'évoquer que ce n'est pas un ensemble.

Yép, mais c'est plus rapide (1/2 lignes) : Ce n'est pas un groupe vu que pas un ensemble.

[kevin237]

oui j ai oublier de preciser que c'etait E vers E et je repete que c 'est un groupe

[Monsieur23]

Qu'est-ce que tu as déjà fait, qu'est-ce qui te bloque ? Ça revient à peu près à écrire la définition de groupe, non ?

[kevin237]

j arrive pas a demontrer l associativiter et a trouver lelement neutre

[Monsieur23]

Il faut montrer que (f o (g o h)) = ((f o g) o h). À quelle condition (nécessaire et suffisante d'ailleurs) deux fonctions sont égales ?

[eratos]

Salut:
a dans G(E) sa (bijection) réciproque a' est évidemment dans G(E) (symétrie) de même que élément neutre (aa'=e). La composée de bijections est bijection (lci) quand à l'associativité: soit x dans E, a b et c dans G(E)
a((bc)(x))= a(b(c(x))) et (ab)c(x)=(a(b(c(x))) par définition. Tout est trop trivial à mon gout

ou alors plus simple l'ensemble des bijections de E sur lui même c'est exactement le groupe symétrique donc c'est un groupe, toujours par définition.

c'est un peu trop vague et farfelu comme explications?