Bonsoir,je coince sur ceci:
Soient A,B deux ensembles et f une aplication de A dans B.Demontrer que les propositions suivantes sont equivalentes:
a)Pour toute partie X de A,f^-1(f(x))=X.
b)f est injective.
Même question pour les propositions suivantes:
c)Pour toute partie Y de B f[f^-1(Y)]=Y
d)f est surjective.
Demonstration
5 messages
- Page 1 sur 1
http://www.cmi.univ-mrs.fr/~rigat/Licence/Corrigeexos0.pdf
Une démonstration est faite fin de la page 1 et début de la 2
Une démonstration est faite fin de la page 1 et début de la 2
Salut,
Vu que ce n'est pas indispensable du tout, à mon avis, il vaut mieux proposer une preuve directe qu'une preuve par l'absurde (ou, par essence même, ce qu'on écrit est... du n'importe quoi...) :
On considère une application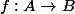
- Supposons que, pour tout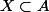 , on ait
, on ait )=X\) et montrons que
et montrons que  est injective.
est injective.
Pour ce faire, considérons deux éléments et
et  de
de  tels que
tels que =f(x_2)) et appliquons notre hypothèse avec
et appliquons notre hypothèse avec 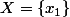 :
:
)=f^{-1}(Y))
Or l'image directe\subset B) n'est autre que
n'est autre que \}) (l'ensemble des images par
(l'ensemble des images par  des éléments du singleton
des éléments du singleton 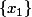 est le singleton
est le singleton \}) ) et, comme
) et, comme =f(x_1)) , on a
, on a \in Y) ce qui signifie (par définition d'une image réciproque) que
ce qui signifie (par définition d'une image réciproque) que ) c'est à dire que
c'est à dire que 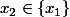 soit encore
soit encore 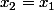 . C.Q.F.D.
. C.Q.F.D.
- Montrons (sans aucune hypothèse) que, pour tout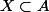 , on a
, on a )) :
:
Soit une partie quelconque de
une partie quelconque de  et
et  un élément quelconque de
un élément quelconque de  . On doit montrer que
. On doit montrer que )) c'est à dire (définition d'une image réciproque) que
c'est à dire (définition d'une image réciproque) que \in f(X)) . Mais cette dernière proprosition est évidente vu que
. Mais cette dernière proprosition est évidente vu que ) est l'image de
est l'image de  qui est dans
qui est dans  .
.
- Montrons que, si est injective alors pour tout
est injective alors pour tout 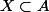 , on a
, on a )\subset X) :
:
On suppose donc injective, on considère une partie quelconque
injective, on considère une partie quelconque 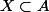 et un élément quelconque
et un élément quelconque )) . On a donc (par définition d'une image réciproque)
. On a donc (par définition d'une image réciproque) \in f(X)) ce qui signifie (définition d'une image directe) qu'il existe un
ce qui signifie (définition d'une image directe) qu'il existe un 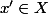 tel que
tel que =f(x')) . Mais comme f est supposée injective, cela implique que
. Mais comme f est supposée injective, cela implique que 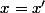 et donc que
et donc que 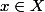 (vu que
(vu que 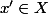 ). C.Q.F.D.
). C.Q.F.D.
Rappel des définition :
- Image directe :
Si est un élément de
est un élément de  et
et  une partie de
une partie de  , "
, ") " signifie qu'il existe un
" signifie qu'il existe un 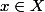 tel que
tel que =y)
- Image réciproque :
Si est un élément de
est un élément de  et
et  une partie de
une partie de  , "
, ") " signifie que
" signifie que \in Y)
Vu que ce n'est pas indispensable du tout, à mon avis, il vaut mieux proposer une preuve directe qu'une preuve par l'absurde (ou, par essence même, ce qu'on écrit est... du n'importe quoi...) :
On considère une application
- Supposons que, pour tout
Pour ce faire, considérons deux éléments
Or l'image directe
- Montrons (sans aucune hypothèse) que, pour tout
Soit
- Montrons que, si
On suppose donc
Rappel des définition :
- Image directe :
Si
- Image réciproque :
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
