Démonstration série de référence

[Anna24]

Bonjour!

Voila je bloque sur une question dans mon chapitre sur les séries de référence:

Montrer que pour tout t appartenant à (0, pi) et tt entier n sup ou égale à 1 on a :
(Somme de 1 à n de cos (kt) ) * sin (t/2) = 1/2 (sin ((2n+1)/2)t) - sin t/2)

Auparavant j'ai résolu la question précédente qui consistait à démontrer que sinx.cosy = 1/2 ( sin(x+y) + sin(x-y) )

Cela doit sans doute servir mais je n'y arrive pas. J'ai essayé de calculer la somme de cos en utilisant la formule de linéarisation, j'ai obtenu somme de exp^kti /2 + somme de e^-kti/2 , étant deux suites géométriques j'ai écrit leur somme de 1er termes, et au final j'obtiens: somme de cos kx = ( cos(t) - cos(tn+t) ) /1 - exp^ti
Je ne suis pas sure que se soit juste.. surtout qu'aprés je reste bloquée quand j'essaye d'effectuer la démonstration en remplaçant la somme de cos kt par ce que je viens de trouver....
Bref je ne suis peut être pas sur la bonne piste... :s

Quelqu'un peut il m'aider s'il vous plait? :help:

Merci beaucoup d'avance! :we:

[girdav]

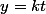
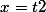
Si on se donne un quelconque entre et et que l'on applique le résultat de la question précédente à et , qu'est-ce que l'on obtient?

[Anna24]

Oui j'ai bien vu qu'on pouvait faire ce parallèle là mais que faites vous de la somme qui se trouve devant cos (kt) ? Comment calculer cette somme?
Merci!

[girdav]

Normalement, une somme télescopique devrait "apparaître".

[Anna24]

ça signifie que Somme de cos (kx) est une suite téléscopique?

Je pensais qu'une suite téléscopique était de la forme: Somme de an+1 - an .....

Si c'est le cas ça nous donne: somme de cos (kx) = cos (nt) - cos (t) ?

Mais ça me parait étrange ^^

[girdav]

On a .

[Anna24]

Ok merci beaucoup!
Mais juste une dernière petite question: pourquoi vous écrivez sin ( -kt + t/2) et non pas sin ( t/2 - kt) ?

[Anna24]

C'est bon oubliez ma question, finalement j'ai compris! Je suis parvenu à la solution j'avais oublié que sin(-a) = - sin (a) ^^
Désolée!! Encore merci pour votre aide! C'est trés gentil d'avoir répondu aussi rapidement!