Bonjour à tous,
Je cherche à démontrer la périodicité d'une fonction

. Et notamment les valeurs qu'elle prend dans un cycle car je sais que certaines valeurs se répètent dans un cycle, donc j'aimerais sortir également le nombre de valeurs différentes sur ce même cycle.
Pour faire cela j'imagine que partir avec un raisonnement sur les suites ne serait pas trop mal. Il faut également savoir que cette fonction cyclique dépend aussi de variables cycles (

,

et

). Voici comment on pourrait le traduire :
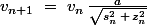
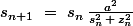
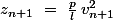
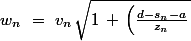^2})
Où

,

et

sont quelconques (rationnels ou irrationnels).
Et cela à partir des conditions initiales où
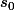
,

(et donc

) sont quelconques mais :
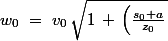^2})
Et enfin,

est défini comme :
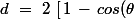 \, \right])
, avec
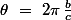
où
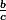
est une fraction rationnelle.
Voilà, si quelqu'un a une illumination...?!
Merci.
