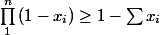 DEMONTRER PAR RECURENCE
DEMONTRER PAR RECURENCEDemonstration par recurence
5 messages
- Page 1 sur 1
Re: demonstration par recurence
Oui. tu as déjà fait des démonstrations par récurrence , tu connais le principe ?
ou bien tu veux qu'on t'explique le principe d'une démonstration par récurrence ?
ou bien tu veux qu'on t'explique le principe d'une démonstration par récurrence ?
Re: demonstration par recurence
hypothèse de récurrence
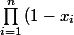 \geq 1-\Sum_{i=1}^{n} \, x_i) (
( )
)
on multiplie par) les deux membres de l'inégalité
les deux membres de l'inégalité
 \Prod_{i=1}^{n} \, (1-x_i) \geq (1-\Sum_{i=1}^{n} \, x_i) (1-x_{n+1}))
...
on multiplie par
...
Modifié en dernier par mathelot le 10 Déc 2020, 14:47, modifié 3 fois.
Re: demonstration par recurence
Bonjour,
Je trouve que Mamy pourrait dire "Bonjour", donner un énoncé complet et montrer qu'il a fait une recherche sur le sujet.
Par ailleurs, est-on sûr que\times(1-4)\times(1-4) \geq 1-3\times 4) ?
?
Je trouve que Mamy pourrait dire "Bonjour", donner un énoncé complet et montrer qu'il a fait une recherche sur le sujet.
Par ailleurs, est-on sûr que
Re: demonstration par recurence
Cette démonstration est valide si les (x_i) sont dans l'intervalle [0;1]
l'inégalité est vraie au rang n+1.
d'où l'hérédité.
j'ai l'impression que cette inégalité n'est pas intéressante
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
