DEMONSTRATION MATRICIELLE
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GEGEJEJE
- Messages: 1
- Enregistré le: 11 Mai 2017, 09:56
-
par GEGEJEJE » 11 Mai 2017, 10:00
Bonjour tous le monde,
En préparant mes examens, je bloque sur un exercice de base ;'( .
Je dois démontrer ceci :
=> Montrer que pour toute matrice A, A X At est une matrice diagonale.
Où At est la matrice transposé de A.
Pourriez-vous me le démontrer mathématiquement?
Merci d'avance
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 11 Mai 2017, 10:18
Salut !
A mon avis, tu as mal formulé ta phrase parce que c'est faux : si je considère dans
)
la matrice
, j'ai
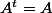
donc
.
-
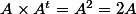
lionel52
- Membre Relatif
- Messages: 274
- Enregistré le: 21 Nov 2012, 22:39
-
par lionel52 » 11 Mai 2017, 10:25
Salut si A est une matrice carrée à coefficients réells
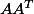
est une matrice diagonalisable (et pas diagonale) car symétrique!
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 11 Mai 2017, 10:31
Oui, je suis d'accord avec
lionel52, c'est plutôt ça qu'il faudrait montrer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
