Démonstration irrationalité de Pi
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
par Romanouch » 20 Jan 2013, 15:56
Bonjour,
Dans le cadre d'une démonstration de l'irrationalité de
, on considère que
est rationnel. On peut donc l'écrire sous la forme d'une fraction de deux nombres entiers a et b.
On considère ensuite:
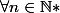
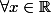
^n}{n!} et P_0(x)=1)
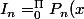sin(x)dx)
Il s'agit de montrer que
> 0
La démonstration que je trouve est la suivante:
\geq0)
Pourquoi x compris entre a et b?alors
est l'intégrale d'une fonction continue, positive et non nulle
(pourquoi non nulle?)On en déduit que
> 0.
Je ne comprends pas pourquoi on dit que la fonction est non nulle.
Bref, je comprends que
mais je ne comprends pas pourquoi
> 0
Merci par avance de votre aide.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 20 Jan 2013, 16:09
Bonjour, :happy3:
Soit
 \in \mathbb{N} \times \mathbb{N}^* $)
:
^n \geq 0 $)
 $)
est non nulle sur
.
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
par Le_chat » 20 Jan 2013, 17:03
C'est pas x entre a et b, c'est x entre 0 et pi=a/b.
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
par Romanouch » 20 Jan 2013, 20:38
barbu23 a écrit:Bonjour, :happy3:
Soit
:
est non nulle sur
.
Bonsoir,
Merci pour ta réponse.
Pourquoi avoir besoin de poser que
?
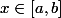
Ne peut-on pas simplement trouver que
^n \geq 0)
pour
?
Dans un cas comme dans l'autre, pourquoi en déduit-on que
> 0? Lorsqu'on intègre entre 0 et
, les valeurs 0 et
ne sont pas prises en compte?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
