[Séries entières] Démonstration de : |a_n| < |b_n| implique

[Wenneguen]

Bonjour,

j'essaye de comprendre la démonstration qui m'est fournie dans un livre de la propriété suivante :


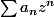
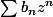
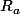
et sont deux séries entières de rayons de convergence respectif et .

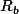
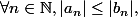
Si alors


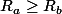
Voici la démonstration qui m'est proposée :

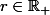
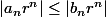
Soit tel que la suite soit bornée. Puisque , la suite est également bornée. On a donc .


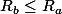
Ce que je ne comprends pas c'est la conclusion en fait : " On a donc . "
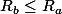
Je suppose que ya une histoire de passage au sup sur , mais tel que je le ferais ça donnerait ...

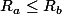
Quelqu'un pourrait-il me détailler un peu la fin ?

Merci ! :zen:

[adrien69]

Bonjour,

j'essaye de comprendre la démonstration qui m'est fournie dans un livre de la propriété suivante :


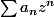
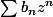
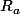
et sont deux séries entières de rayons de convergence respectif et .

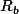
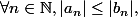
Si alors


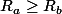
Voici la démonstration qui m'est proposée :

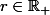
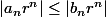
Soit tel que la suite soit bornée. Puisque , la suite est également bornée. On a donc .


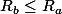
Ce que je ne comprends pas c'est la conclusion en fait : " On a donc . "
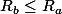
Je suppose que ya une histoire de passage au sup sur , mais tel que je le ferais ça donnerait ...

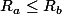
Quelqu'un pourrait-il me détailler un peu la fin ?

Merci ! :zen:

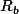
Eh bien si tu appelles le rayon de ta deuxième série, et que tu as comme tu le dis presque qui est bornée alors le rayon de ta série associée à ne peut qu'être plus grand ou égal à celui de ta série associée à sans quoi tu aurais qui ne serait pas borné puisque

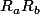
J'ai été clair ou bien je recommence ?

[Wenneguen]

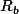
Eh bien si tu appelles le rayon de ta deuxième série, et que tu as comme tu le dis presque qui est bornée alors le rayon de ta série associée à ne peut qu'être plus grand ou égal à celui de ta série associée à sans quoi tu aurais qui ne serait pas borné puisque

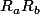
J'ai été clair ou bien je recommence ?

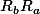
Ok je crois que j'ai compris, mais à la fin tu voulais dire " puisque qu'on aurait ", non ?

[adrien69]

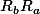
Ok je crois que j'ai compris, mais à la fin tu voulais dire " puisque qu'on aurait ", non ?

Oui, désolé pour la tournure elliptique

[Wenneguen]

Oui, désolé pour la tournure elliptique

Et surtout l’interversion de a et b ! ^^

[adrien69]

Et surtout l’interversion de a et b ! ^^

Ah oui ! Ooops...
Faut me comprendre, aujourd'hui je bosse de l'algèbre : représentations de groupes, modules, corps finis, toussa toussa. Je suis pas vraiment en mode analyse là

[Le_chat]

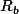
Eh bien si tu appelles le rayon de ta deuxième série, et que tu as comme tu le dis presque qui est bornée alors le rayon de ta série associée à ne peut qu'être plus grand ou égal à celui de ta série associée à sans quoi tu aurais qui ne serait pas borné puisque

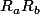
J'ai été clair ou bien je recommence ?

Pourquoi est-ce que (an*Rb^n) serait borné?

[adrien69]

Pourquoi est-ce que serait borné?

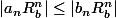
On a pour tout n par hypothèse.

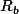
Or est bornée par définition de (qui est le sup des R tel que blabla), on en déduit directement que est bornée.

[Le_chat]

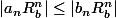
On a pour tout n par hypothèse.

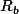
Or est bornée par définition de (qui est le sup des R tel que blabla), on en déduit directement que est bornée.

Si on prend la série entière somme des x^n de rayon 1, je pense pas que la somme des 1 soit bornée :p

[Le_chat]

Si on prend la série entière des nx^n, son rayon est bien 1, pourtant (n) n'est pas bornée.

[Wenneguen]

Si on prend la série entière des nx^n, son rayon est bien 1, pourtant (n) n'est pas bornée.

Le fourberies du sup ! ^^ Tu as une réponse Le_chat ?

[lionel52]

On pose A = {r > 0 tel que (an.r^n) est bornée} et B = {r > 0 tel que (bn.r^n) est bornée}
Ra = sup(A) et Rb = sup(B)
Soit r € B, on a |bn.r^n| >= |an.r^n| donc comme (bn.r^n) est bornée, (an.r^n) aussi et r € A

Donc on a que B C A donc du coup sup(A) >= sup(B)

[Le_chat]

Ben tu veux montrer que Rb est inférieur à Ra. Si tu utilises le fait que Rb=sup(r dans R tel que |bn*r^n|est borné}. Tu prends r dans R. Si |bn*r^n| est borné, |an*r^n| est borné car c'est plus petit.
Donc {r dans R tel que |bn*r^n| est borné} est inclus dans {r dans R tel que |bn*r^n| est borné},et le sup du premier, Rb , est plus petit que le sup du second, Ra.

Grilled.

[adrien69]

Ah oui ! Je suis con. Mes excuses.