Voici la dérivée partielle d'une fonction
La fonction
La dérivée :
en posant
De mon côté, je trouve :
Démonstration à un facteur positif près...
1 message
- Page 1 sur 1
Démonstration à un facteur positif près...
par Aud39 » 01 Nov 2011, 18:27
Bonjour,
Voici la dérivée partielle d'une fonction)
par rapport à 
à un facteur positif près, que je n'arrive pas à retrouver. Pourriez-vous m'aider SVP et surtout me dire concrètement ce que signifie "à un facteur positif près"? Merci !
La fonction
:
+[(y_{2}^{2}-y_{1}^{2})^{2}+16(y_{2}-y_{1})(q_{2}-q_{1})]^{\frac{1}{2}}}{12(y_{2}-y_{1})(q_{2}-q_{1})})
La dérivée :
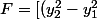en posant^{2}+16(y_{2}-y_{1})(q_{2}-q_{1})]^{\frac{1}{2}})
, on obtient "à un facteur positif près":
 \left[(y_{2}^{2}-y_{1}^{2})+F-\frac{24((y_{2}-y_{1})(q_{2}-q_{1})}{F} \right])
De mon côté, je trouve :
}{12(y_{2}-y_{1})(q_{2}-q_{1})^{2}}-\frac{2}{3F(q_{2}-q_{1})})
Voici la dérivée partielle d'une fonction
La fonction
La dérivée :
en posant
De mon côté, je trouve :
1 message
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :