Demonstration de l'existence du centre d'inertie

[vik21]

Bonjour, je n'arrive pas à comprendre ou plutôt à démontrer l'existence du centre d'inertie d'un objet. Pourquoi le centre d'inertie est il le point commun de tout les axes équilibrant les moments?

Si je pince du bout des doigts un objet plat type équerre mais plein.. et que cet objet tourne sur lui-même jusqu'à trouver son équilibre, sans relâcher les doigts si je tourne à nouveau cet objet, il pivotera à nouveau autour de ce point pour retrouver cet état bon... On peut tracer un axe passant par ce point et déterminé par la direction de la force de pesanteur.
Mais qu'est ce qui me prouve hormis l'observation... qu'est ce qui démontre qu'il existe vraiment un point (centre d'inertie) commun à tout ces axes, possibles et imaginables par cet expérience si je devais pincer l'objet en chacun de ses points, et que ce point commun permette de le faire tourner sans relâcher les doigts et sans qu'il ne cherche à atteindre un état d'équilibre autre que celui dans lequel je le positionne?

Est-ce que c'est un axiome physique et géométrique comme la propriété des leviers? Allez savoir pourquoi un levier fait levier... J'aimerai comprendre un peu mieux, y a-t-il une démonstration autre que : "tu vois bien qu'ils se coupent!!!".
Parce qu'on pourrait m'avoir dit que tout ces axes ne se coupent pas, je l'aurai assimilé aussi bêtement que tout le reste des théorèmes physiques et mathématiques. Alors je fais l'effort de m'intéresser...

Merci pour votre aide.

[ampholyte]

Bonjour,

Tu as sûrement étudié les baricentres. Le centre d'inertie est donc le centre des masses d'un objet.

Pour un système de n points matériels discrets assortis de leur masse (Mi, mi;)) avec 1 i n



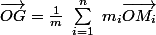
Je te conseille également de lire cet article : http://fr.wikipedia.org/wiki/Barycentre_(physique)

[adrien69]

Dans le cas d'un champ de gravité uniforme (comme dans ton expérience de pensée), centre d'inertie et centre de gravité sont confondus, c'est-à-dire que le centre d'inertie est le point auquel s'applique la résultante du poids. En particulier quand ton objet est suspendu à l'équilibre, la force que tu exerces pour le maintenir est colinéaire au poids (du fait du théorème fondamental de la dynamique) et possède en plus la même droite d'action car sinon un effet de levier se ferait ressentir (du fait du théorème du moment cinétique).
L'effet de levier étant pour faire simple ce qui fait que les grues basculent : même si les forces qui s'appliquent (poids de ce qui est soulevé et réaction du support de la grue) sont colinéaires, elles vont avoir tendance à vouloir se rapprocher pour avoir la même droite d'action (d'où les contreforts des cathédrales, ou de façon plus récente et plus dramatique, la deuxième grue qui maintient la première à Brétigny-sur-Seine).

[nodjim]

vik21 se pose une drôle de question. Imaginons un objet plan (une plaque quelconque). On trace 3 diagonales sécantes qui reflètent chacune un équilibre axial de l'objet. Si ces 3 diagonales ne se coupaient au même endroit, quelles seraient les conséquences ?

[Kikoo <3 Bieber]

Yo à tous !

Ampholyte, je pense qu'on préfèrera la version continue ;)

[adrien69]

vik21 se pose une drôle de question. Imaginons un objet plan (une plaque quelconque). On trace 3 diagonales sécantes qui reflètent chacune un équilibre axial de l'objet. Si ces 3 diagonales ne se coupaient au même endroit, quelles seraient les conséquences ?

La masse (ou plutot le poids) serait excédentaire. En brefdeux solutions seraient envisageables : le champ de gravité ne serait pas uniforme, ou bien les lois de la physique ne seraient pas les mêmes en tous les points de ton expérience

[vik21]

merci nodjim d'avoir rendu ma question nettement plus concise.

Ampholyte, je n'ai pas étudié les barycentres... je suis en train de les étudier et de bloquer sur la première propriété...

Merci mais les articles mathématiques wikipédia sont trop rigoureux pour un novice comme moi et trop ornés de textes superflues énumérant les particularités existantes mais impertinentes avec un niveau mathématique supérieur autour de concepts simples et supposés à la portée de tous. Rien de mieux pour larguer les gens dès les première lignes.

C'est comme si je te racontais ma journée en commençant par t'expliquer tout ce qu'on peut faire dans une journée... Puis par tout ce que je pouvais faire, en commençant cet journée.. comprenant toutes ces choses que j'aurai pu faire MAIS que je ne fis pas, formant un ensemble distinct des choses que je n'aurais pas pu faire de toutes manières... (ET que je ne fis pas...) Et toi ta journée?