Démonstration ecriture décimale qui termine

[Argentoratum]

Je n'arrive pas à montrer que si q s'écrit 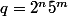avec n,m entier naturelle, alors pour tout p entier naturelle, 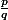a une écriture décimale qui termine.

J'ai l'impression que c'est lié au fait que l'on soit en base 10 et que 2 et 5 divisent 10, mais je ne saurais pas le prouver et j'ai du mal à transposer la situation dans une autre base pour vérifier que mon hypothèse est vraie et donc continuer dans cette voie.

[leon1789]

Tu as raison : le développement décimal de a/b s'arrête si et seulement si b = 2^k 5^j . On peut aussi caractériser cela en disant que l'on peut écrire a/b sous la forme c/10^n.

En base B, on a le résultat similaire : le développement de a/b s'arrête si et seulement si a/b peut s'écrire c/B^n

Pour voir cela, il suffit d'avoir un algorithme de développement décimal en base 10, puis de changer les 10 en B...

[Argentoratum]

Tu as raison : le développement décimal de a/b s'arrête si et seulement si b = 2^k 5^j .

C'est l'objet de la question suivante avec ((a;b)=1).

le développement de a/b s'arrête si et seulement si a/b peut s'écrire c/B^n

C'est donc une propriété, faut-il quand même le démontrer?

Pour l'algorithme de développement, je ne vois pas comment faire.

[Doraki]

Qu'est-ce que tu peux dire de p/q quand q est une puissance de 10 ?

[digardel]

Y a une erreur dans ton énoncé .Ca doit etre q = 2^n*5^m car sinon avec n=1 m=1 et q=3 alors p/q=10/3. Et le cas q= 2^n*5^m c est presque évident

[Argentoratum]

Oui je me suis trompé, c'était 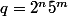, j'ai réctifié dans le post.

Qu'est-ce que tu peux dire de p/q quand q est une puissance de 10 ?

Que p/q a une ecriture decimale qui termine, mis là on a .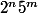
Au mieux je peux dire que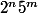 peut s'écrire de la forme 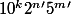avec k = min(n,m) avec soit n' = 0 et m' = m-n ou soit n' = n-m et m' = 0.

Enfin je sais pas si j'ai étais clair.

Mais de là à dire que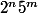 est une puissance de 10, je ne vois pas.

[digardel]

mutiplie le deno et le num de p/q par une puissance de 10 d exposant bien choisi et c est fini

[Argentoratum]

par une puissance de 10 d exposant bien choisi

Je ne vois par quel puissance de 10 je pourrais le faire.

Mais si je multiplie par 2^m 5^n, j'obtient :

p 2^m 5^n / 2^n 5^m 2^m 5^n = p 2^m 5^n / 10^n+m .

Est ce que ça ressemble à ce que tu attendais?

[Doraki]

Oui c'est ça, il y a une puissance de 10 qu'est multiple de ton dénominteur donc en la faisant apparaitre, tu vois que l'écriture de la fraction se termine.

2^n 5^m 2^m 5^n ça fait 10^n+m

[digardel]

çà marche aussi je pensais a multiplier num et deno par
10 ^(n+m) = 2^n+m * 5^n+m c était un chouia plus rapide

[Doraki]

Mais en disant ça, implicitement tu comptes faire des simplifications nan ?

[Argentoratum]

Ok merci beaucoup, mais une fois que j'ai mis la fraction sous forme d'une fraction avec une puissance 10 comme denominateur, est ce que je peux conclure directement ou il faut le démontrer et là j'en reviens à ma question un peu plus haut :

le développement de a/b s'arrête si et seulement si a/b peut s'écrire c/B^n

Est une propriété ou c'est à démontrer.

[Doraki]

ben l'écriture de a/10^n s'arrête parceque c'est juste a déplacé de n vers la droite.
donc si p/q = a/10^n, l'écriture de p/q s'arrête aussi.
c'est le même nombre il a la même écriture décimale.
Normalement tu peux conclure pour la question 1.

Tu veux montrer la réciproque du "si et seulement si" ?
Elle est encore plus facile puisque si t'as une écriture décimale qui s'arrête il suffit juste de lire le nombre a et de compter le nombre n de chiffres après la virgule pour avoir a/10^n.

[Argentoratum]

OK, merci beaucoup

Oui c'est cela. La question précise est :
Si p,q entiers naturelles et (p;q) = 1 alors p/q a une écriture decimale qui termine si et seulement si q = avec n,m entiers naturelles.

[Doraki]

Ah je parlais pas de la question 2 mais de "le développement de a/b s'arrête si et seulement si a/b peut s'écrire c/B^n "

[Argentoratum]

Désolé je ne vois pas ce que tu veux dire.
On sait que p/q se termine, mais comment en déduire que q de la forme ?

[Argentoratum]

Désolé d'avoir créé un décalage dans la discussion.

Pour

"le développement de a/b s'arrête si et seulement si a/b peut s'écrire c/B^n "

Si tu a une démonstration formelle je suis preneur, mais dans le cadre de cet exercice est ce que c'est à démontrer?

Et pour la question suivante de mon exercice

Si p,q entiers naturelles et (p;q) = 1 alors p/q a une écriture decimale qui termine si et seulement si q = avec n,m entiers naturelles.

Je disais que :

On sait que p/q se termine, mais comment en déduire que q de la forme ?

J'espère que c'est un peu plus clair.

[Doraki]

Désolé d'avoir créé un décalage dans la discussion.

Pour [...]
Si tu a une démonstration formelle je suis preneur, mais dans le cadre de cet exercice est ce que c'est à démontrer?

Ca dépend de toi et de comment tu formaliserais "avoir une écriture décimale finie" ou "écriture décimale d'un nombre".
Moi, cette phrase me convient pour une définition de "avoir une écriture décimale finie".

Et pour la question suivante de ton exercice.

Si p/q = p'/10^n, avec p et q premiers entre eux, t'en déduis quoi sur q ?

[Argentoratum]

Je suis désolé mais je ne vois vraiment pas.

[Doraki]

Comment tu trouves la forme réduite d'une fraction a/b qui n'est pas irréductible ?