Démo par l'absurde

[mimi59]

Bonsoir à tous,
voilà je me pose une petite question qui très certainement peut paraitre simple pour vous,en ce qui concerne la démonstration par l'absurde,que j'aimerai utiliser de façon très rigoureuse:

on part d'une hypothèse (H)
à partir de là on raisonne à partir des données et de (H)

et ensuite on arrive à (I) quelque chose d'impossible (absurdité).
et donc là on dit que notre hypothèse de départ est alors fausse.

est-ce bien cela? ou plutôt au lieu de (I),on cherche à aboutir à une contradiction avec notre hypothèse de départ.

désolée si ce n'est pas clair.
j'aimerais juste connaitre le principe de la démonstration par l'absurde de façon précise. où doit intervenir(et comment) mon hypothèse de départ?

merci d'avance!

[jose_latino]

On va pense qu'il faut démontrer qu'une proposition, de type: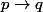
Démontrer ça veut dire: démontrer que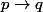 est une tautologie (c'est toujours vrai). La démonstration par l'absurde s'agit d'écarter l'unique posibilité de que c'est proposition soit fausse: et

La démonstration directe est écarter que c'est proposition soit fausse, mais en éprouvant que si donc est jamais faux.

[mimi59]

merci mais je ne comprends pas trop...
si je prends comme exemple: démontrer que l'ensemble des nombres premiers est infini.
je raisonne par l'absurde: je suppose alors que l'ensemble des nombres est fini...

dans ce cas qu'est-ce que p et q,comme tu l'expliques? :hein:

dans cet exemple,que faut-il faire?aboutir à une contradiction avec l'hypothèse de départ ou est-ce qu'une absurdité suffit (du genre je trouve un nombre premier=1 impossible)?? :hein:

merci d'avance!

[jose_latino]

merci mais je ne comprends pas trop...
si je prends comme exemple: démontrer que l'ensemble des nombres premiers est infini.
je raisonne par l'absurde: je suppose alors que l'ensemble des nombres est fini...

dans ce cas qu'est-ce que p et q,comme tu l'expliques? :hein:

P="S est l'ensemble de nombres premiers"
Q="S est infini"
C'est un peu artificiel, mais on a donné la forme "P->Q".

[alben]

Bonsoir,

De manière plus simple, le raisonnement par l'absurde consiste à dire : on suppose fausse la propriété P que l'on veut prouver et avec cette supposition, on arrive à une contradiction de l'hypothèse de départ, des données du problème ou encore d'un théorème connu.
Plus précisément on peut dire que l'on raisonne à partir de 3 systèmes de propositions supposées vraies :

• A = les axiomes de bases mathématiques et tous les théorèmes qui en découlent
• H= les hypothèses ou données du problème : le contexte
• non P= l'hypothèse du raisonnement par l'absurde dont on veut montrer qu'elle est fausse (et donc que P est vraie)

A partir de tout cela, il suffit d'arriver à une contradiction quelconque pour que P soit prouvé.
Le plus souvent, on montre que l'une de hypothèses de H n'est pas vérifié ou que (nonP)==>P mais cela peut être aussi une propriété indépendante de l'énoncé, du genre 4 est premier.

[rene38]

Bonsoir

Un grand classique : démontrer que

[mimi59]

ok!merci bcq à tous! c'est plus clair dans mon esprit!
merci!!