Demande de reference

[ThomasM]

Bonjour à tous,

Je prépare l'Agrégation de mathématiques, et je cherche deux références.
Je voulais savoir ou est ce que je pouvais trouver le théorème de Brouwer avec une démonstration correcte.
Ensuite en application j'ai pris connaissance d'un théorème qui nous dit a peu près cela :
"Dans un triangle quelconque l'application projection orthogonale sur un coté opposé ittéré trois fois admet un unique point fixe (cela signifie que si on prend un point sur un coté du triangle, qu'on le projecte orthogonalement sur un coté opposé et qu'on réitere ce procedes 3 fois, il y a un unique point ou on retombe sur le point de depart !).
Je voulais savoir tout d'abord l'enoncé exact de ce théoreme et s'il était réferencé dans un livre avec sa demonstration.

Je vous remercie par avance.
Cordialement
Thomas

[busard_des_roseaux]

bonjour,

j'espère que ces quelques références t'aideront
prépa agreg

Brouwer

Pour la projection orthogonale, as tu essayé d'écrire , en complexes, les affixes des sommets ?
une equation de droite est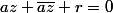 avec r réel

très cordialement,

[ThomasM]

Bonjour,
tout d'abord je tiens a m'excuser pour le retard...
En effet la semaine je n'est pas internet, et je suis pas mal occupé.
Merci pour les liens fournies, ils m'ont été tes utile.
Ensuite pour la demonstartion pour le triangle, un prof m'a donne une solution qui utilise le theoreme du point fixe de Picard.
Par contre, si j'utilise les nombres complexes, je peut mettre ce théoreme dans d'autres lecons.
Du coup, je vais essayer de faire comme vous me le conseille avec les affixes.

Donc si jai bien compris, je dois prendre comme repere (AB,AC) tout le temps, ou a chaque fois je change de repere? Ensuite que dois faire, ecrire les coordonnees de A, B et C? puis apres, la projection orthogonale est definie comme etant le produit scalaire euclidien nul entre AH et BC (H projete orthogonal de A sur BC) ....