Degré topologique

[Math_sup]

Bonjour
J'ai ce petit exercice.

Soit un ouvert borné de et .
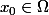
On suppose qu'il existe tel que : si pour
alors .
Montrer que admet un point fixe.
En déduire que si et pour tout
alors admet un point fixe.

Qui peut m'aider à le résoudre ?
S'il vous plait, merci.

[adrien69]

Salut,
Tu es sûr que tes hypothèses sont toutes là ?
Ta condition équivaut à ce que si l'image d'un point est sur la droite (x,x0) alors elle est sur le segment. Soit, mais je n'arrive pas à l'utiliser, quelle que soit ma façon de tripatouiller ce bidule.
Après il est aussi possible que je n'aie pas vu le truc, mais bon autant vérifier ;)