Définition et unicité du nombre compplexe i

[leon1789]

Merci ! En fait je l'ai vu au début de l'année (enfin très vite en exercice de cours) et je ne m'en rappelais plus (en fait je dois dire qu'à l'époque je n'avais pas compris) !
Bon alors j'ai cherché dans mes notes :
|
La multiplication marche bien comme dans les complexes, ainsi que l'addition. De plus tout élément s'écrit de façon unique:

Donc et

Merci beaucoup !

Oui, mais le problème est de justifier la "forme" de la matrice.

Et là, c'est peut-être mettre la charrue avant les boeufs :
la matrice ne serait-elle pas avant tout la matrice de l'application de multiplication par a+ib dans le R-base 1,i de C

[Lemniscate]

peux pas rester sérieux 3 minutes !!!

Lol ben en fait même si c'est pas des matrices antisymétriques que j'avais vu, c'était quand m^me des matrices 2x2, donc merci de m'avoir mis sur la voie ! Je sais pas si c'était volontaire mais merci !

[Lemniscate]

Et là, c'est peut-être mettre la charrue avant les boeufs :
la matrice ne serait-elle pas celle de la multiplication par a+ib dans le R-base 1,i

En fait c'est celle de la multiplication par a-ib :king: lol

Mais sinon je vois pas pq c'est un problème, ce que tu dis est vrai mais je n'ai pas besoin de passer par la base (1,i) de C pour définir ma matrice ! Je ne passe que par R et par les matrices!

[ThSQ]

Ben, le passage au quotient A[X]/(X²-a), c'est tout aussi efficace.

Et dans le cas non intègre ?

[leon1789]

En fait c'est celle de la multiplication par a-ib :king: lol

argh :briques: :zen: j'ai toujours confondu i et -i ! lequel est positif ?...

Mais sinon je vois pas pq c'est un problème, ce que tu dis est vrai mais je n'ai pas besoin de passer par la base (1,i) de C pour définir ma matrice ! Je ne passe que par R et par les matrices!

Et si on change la relation x^2=-1 pour d'autre(s) relation(s) algébrique(s) : tu pourras facilement construire un anneau de matrices satisfaisant ?

Et dans le cas non intègre ?

:hein: B := A[X]/(X^2-a) est un anneau contenant A , que ce dernier soit intègre ou pas.

[Lemniscate]

Et si on change la relation x^2=-1 pour d'autre(s) relation(s) algébrique(s) : tu pourras facilement construire un anneau de matrices satisfaisant ?

Ben ca dépend, donne moi une relation et j'essaierai...
Par exemple si on remplace x^2=-1 par x^2=p où p négatif, tu remplace par . Bon ok j'ai pris un exemple facile mais j'ai du mal à imaginer d'autres relations ...

[mathelot]

Bjr,

juste pour dire que si l'on ne peut distinguer i de -i, déja était défini à isomorphisme près, idem pour ,,

[yos]

est le nombre a tel que a²=2 et tel que a soit positif. Je ne vois pas en quoi ca pose un problème.

Ca pose aucun problème, je te le fait pas dire.
Mais il en va de même pour i=(0,1) et pas (0,-1).
L'ensemble C se construit à partir de l'ensemble R. A un moment donné, tu fais un choix pour définir i. Exactement comme tu fais le choix de dire que est la solution positive de x²=2.
Quelle que soit la construction choisie, il faudra bien définir i clairement.

[leon1789]

Ben ca dépend, donne moi une relation et j'essaierai...

Disons un anneau A contenant Q = frac Z, et tel que le polynôme se factorise complètement en produit de ? ...avec des matrices à coefficients dans Q :hein:

[Doraki]

Ben tu prends le corps de décomposition de X^5+X+1, qui est un Q-ev de dimension finie, et donc tu peux interpréter chaque élément x par la matrice de multiplication par x.
Par contre, je calculerais pas tout ça à la main.

[leon1789]

Ben tu prends le corps de décomposition de X^5+X+1, qui est un Q-ev de dimension finie, et donc tu peux interpréter chaque élément x par la matrice de multiplication par x.
Par contre, je calculerais pas tout ça à la main.

Ok ! c'est exactement ce que je pense : on construit d'abord l'anneau qui fait ce qu'il faut, puis on monte un anneau de matrices collant à la situation. C'est ce que je disais au-dessus avec la matrice

D'autre part, comment > ? En quotientant Q[a1,a2,a3,a4,a5] par les 5 relations provenant de l'identification de (x-a1)...(x-a5) = x^5+x+1. Dans ce quotient , le polynôme x^5+x+1 se décompose totalement par construction !
(en général, cette construction ne donne pas un corps, mais sur cet exemple, c'est effectivement un corps... pas tout a fait évident à prouver)

Maintenant, si on monte des matrices sur cet exemple comme l'a rappelé (EDIT Doraki , on obtient des matrices à 5! = 120 lignes et colonnes (dimension du corps de décomposition de x^5+x+1 sur Q) ... Mais en faisant autrement, par un moyen totalement différent, on peut surement faire nettement mieux.

[Lemniscate]

Au fait j'ai enfin compris que si on définit C avec un isomorphisme f (en même tps d'ev et d'anneaux) alors i=f(a) et f(-a) vérifiera aussi f(-a)^2=f((-a)^2)=f(a^2)=f(a)^2=-1 !

Donc j'ai compris vos histoires de "choix" nécessaires mais qui ne changeront pas les résultats qu'on obtiendra en travaillant ds C !

Merci

[mathelot]

Mais il en va de même pour i=(0,1) et pas (0,-1).
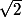
L'ensemble C se construit à partir de l'ensemble R. A un moment donné, tu fais un choix pour définir i. Exactement comme tu fais le choix de dire que est la solution positive de x²=2.
Quelle que soit la construction choisie, il faudra bien définir i clairement.

Bonjour, tu pourrais préciser ? je n'ai pas les idées très claires là-dessus
(sur le reste non plus :zen: ) . Parce que effectivement, on pose i=(0,1)

Mais à la fin de la construction, on conclue par: le corps est unique , à isomorphisme unique près. Je ne vois pas du tout comment on peut distinguer i de -i.

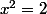
Pour l'ensemble des solutions réelles de l'équation est ordonné. est la plus grande de ces solutions.

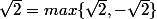
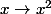
si l'on trace la courbe de et que l'on inverse
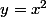
la relation , on va, en partant de l'axe vertical, vers la droite, sur l'axe horizontal, pour aller chercher

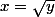
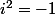
pour aller chercher i à partir de , on va chercher i au dessus de l'axe réel et pas en dessous de cet axe, ce qui est possible car le plan euclidien est orienté. mais il se trouve que
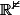
a une orientation canonique car (1,0),(0,1) est une base naturellement directe.

mais les gauchers devraient poser i=(0,-1) ? :doh:

[yos]

Mais à la fin de la construction, on conclue par: le corps est unique , à isomorphisme unique près. Je ne vois pas du tout comment on peut distinguer i de -i.

Mélangeons pas isomorphisme et automorphisme.
Quand tu parles du groupe V4, c'est toujours à isomorphisme près. Maintenant, si tu prends le groupe des isométries d'un certain rectangle tu trouves "un" V4 et tu n'es plus "à isomorphisme près". Chacun de tes éléments a un nom bien déterminé. Mais pour les distinguer algébriquement, i.e. uniquement par leurs propriétés de composition, ben c'est impossible (sauf pour l'identité) parce que ton groupe a des automorphismes non triviaux.
Pour C c'est pareil. Mais quand tu construis C, le "i" a un sens bien précis. On peut pas le confondre avec -i. Ensuite tu réalises que d'un point de vue purement algébrique, ils ont les mêmes propriétés. Tu traduis ça en disant que la conjugaison est un automorphisme et c'est tout.

[Doraki]

Maintenant, si on monte des matrices sur cet exemple comme l'a rappelé yos, on obtient des matrices à 5! = 120 lignes et colonnes (dimension du corps de décomposition de x^5+x+1 sur Q) ... Mais en faisant autrement, par un moyen totalement différent, on peut surement faire nettement mieux.

Ca m'étonnerait qu'on puisse faire mieux.
Je pense que si on a un corps L de matrices de Mn(K) alors [K:L] <= n (voire n est un multiple de l'indice).

[ThSQ]

:hein: B := A[X]/(X^2-a) est un anneau contenant A , que ce dernier soit intègre ou pas.

M'semblait qu'y avait un blème dans le cas non intègre. Bon j'ai dit une c*nerie (mais je vérifierai quand même ce week-end !)

[leon1789]

Ca m'étonnerait qu'on puisse faire mieux.
Je pense que si on a un corps L de matrices de Mn(K) alors [K:L] <= n (voire n est un multiple de l'indice).

Oui, c'est exact.

[leon1789]

Bon j'ai dit une c*nerie

oui, c'est exact :ptdr: (pour une fois !)