Bonjour à tous.
Voilà la définition d'une fonction dont la limite vaut 0 quand x tend vers +oo :
Une fonction f tend vers 0 en +oo si elle est définie au voisinage de +oo et si l'on a :
pour tout epsilon > 0, il existe A appartenant à R tel que pour tout x appartenant à Df ( domaine de def ) , si x > a alors cela implique que valeur absolue de f(x) < epsilon.
Est-ce que cela veut donc dire que epsilon = f(A) ?
Merci d'avance.
PS : désolé mais je ne sais toujours pas comment écrire en langage mathématique sur le forum.
Définition d'une limite
6 messages
- Page 1 sur 1
[quote="Nass-nass93"]Bonjour à tous.
Voilà la définition d'une fonction dont la limite vaut quand
quand  tend vers
tend vers  :
:
Une fonction tend vers
tend vers  en
en  si elle est définie au voisinage de
si elle est définie au voisinage de  et si l'on a :
et si l'on a :
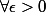 ,
,  ,
, 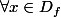 ( domaine de de
( domaine de de  ) , si
) , si  alors
alors  \mid 0) . En revanche, tu peux choisir, si ça te chante, et pourvu que
. En revanche, tu peux choisir, si ça te chante, et pourvu que ) soit strictement positif,
soit strictement positif, 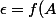)
Voilà la définition d'une fonction dont la limite vaut
Une fonction
sos aide svp
on a une fonction F(x)= (SIN x )/ ( 2cosx - 1 )
jai calculé ma dérivée F'(x) = (2-cosx) / (2cosx - 1 ) 2
et on me demande de déduire quand est ce ke la la fonction sera croissante et décroissante , jai étudié l'équation F(x) = 0 on a : 2 - cos x = 0 mais jarrive plus à continuer .
merci bien
jai calculé ma dérivée F'(x) = (2-cosx) / (2cosx - 1 ) 2
et on me demande de déduire quand est ce ke la la fonction sera croissante et décroissante , jai étudié l'équation F(x) = 0 on a : 2 - cos x = 0 mais jarrive plus à continuer .
merci bien
@rodriguez90
Cette fonction étant 2 périodique et impaire sur quel intervalle ?
périodique et impaire sur quel intervalle ?
tu veux faire l'étude de cette fonction ?
Si f(x)= sinx/(2*cosx-1)
OUI : le calcul de la fonction dérivée donne f'(x)= (2-cosx) / (2cosx - 1)^2
DONC le signe de f'(x) est le signe de l'expression 2-cosx
qui d'après moi est constant et est toujours POSITIF
donc la fonction f sur un intervalle "donné" est STRICTEMENT CROISSANTE
Cette fonction étant 2
tu veux faire l'étude de cette fonction ?
Si f(x)= sinx/(2*cosx-1)
OUI : le calcul de la fonction dérivée donne f'(x)= (2-cosx) / (2cosx - 1)^2
DONC le signe de f'(x) est le signe de l'expression 2-cosx
qui d'après moi est constant et est toujours POSITIF
donc la fonction f sur un intervalle "donné" est STRICTEMENT CROISSANTE
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
