Définition d'un nombre premier irrégulier

[anthony_unac]

Bonjour,

En consultant le net, on trouve une définition précise mais peu évidente d'un nombre premier régulier. En essayant de regrouper ces infos et en prenant l'opposé de ceux ci j'en arrive à la définition suivante :

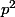
Un nombre premier est irrégulier si et seulement si divise au moins une des sommes pour

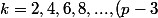Cette définition est elle exacte ?

[zygomatique]

salut

et si tu nous donnais déjà la définition d'un nombre premier régulier ?

[anthony_unac]

Alors voici la définition la plus courante d'un nombre premier régulier mais comme je le disais elle est franchement indigeste pour les amateurs de ma trempe :

Un nombre premier impair est dit régulier s'il ne divise pas le nombre de classes du corps cyclotomique ℚ(ζp), où ζp est une racine primitive p-ième de l'unité.

Une autre définition :
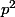
Un nombre premier impair est régulier si et seulement si ne divise aucun des nombres pour

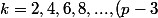[zygomatique]

ben alors ta définition est exacte puisque tu as pris la négation de "une autre définition" ....

[anthony_unac]

Ok pas de soucis donc la négation est la bonne.
Merci pour cette confirmation