Définition espace analytique

[Archytas]

Bonsoir,
Y a-t-il une différence entre "espace analytique" et "variété complexe" ? Je trouve pas grand chose sur les espaces analytiques sur internet mais dans un livre l'auteur parle que de ça. Il semble les traiter comme des variétés complexes mais je voudrais être sûr.
Merci !

[Archytas]

Pour que ça soit plus clair je vous fournis le PDF en question : (premier lien sur google https://www.google.it/?ion=1&espv=2#q=espaces%20de%20stein)
Et j'en profite pour poser deux question concernant les notations :
1) p.3 du PDF que représente la notation "inclu inclu" dans le théorème 1.3 ?
2) p.4 du PDF que représentent les ?
Etant donné que le PDF n'est qu'une partie d'un livre (il commence p.190) les notations doivent être expliquées avant mais je n'ai trouvé que cette partie du livre.
Merci d'avance pour votre aide

[Robot]

Les définitions varient suivant les textes.

Pour c'est sans doute "relativement compact dans".

Et désigne habituellement l'anneau des sections du faisceau 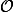sur .

[Archytas]

Ok super merci ! Et pour vous espace analytique c'est bien une variété complexe ?

[Robot]

Ca dépend, je te dis. Des fois oui, des fois non. Il faut voir les définitions utilisées dans le texte.

[Archytas]

Ok merci, et autre chose, j'essaie de démontrer le Lemme 2.1 ne serait ce qu'en dimension 1, qu'a pas l'air méchant. Pour un x dans X, la condition de séparation holomorphique nous indique qu'il existe g non constante qui s'annule en x. Et du coup V(g) l'ensemble des zéros de g est de dimension 0 donc c'est un espace discret de X. Ensuite je suppose par l'absurde que pour toute fonction holomorphe f s'annulant en x on a V(g,f) de cardinal supérieur à 2 et je voudrais arriver à une contradiction, mais ça coince. Des idées ?

[Robot]

Je ne sais pas de quel texte tu parles.

[Archytas]

Le premier PDF https://www.google.it/?ion=1&espv=2#q=espaces%20de%20stein
Le lemme est : Soit X un espace analytique holomorphiquement séparé de dimension n alors

[Robot]

C'est un articlede Math. Ann. que je ne peux pas voir de chez moi

[Archytas]

Ah zut, il s'agit juste de montrer le lemme énoncé juste au dessus sous l'hypothèse que X est holomorphiquement séparé, c'est à dire que