Si je compte les bijections d'un ensemble a n+1 elements dans lui meme.
La formule des factoriels donne (n+1)!=n!*(n+1).
Donc cela impliquerait que le nombre de bijection d'un ensemble dans lui meme s'obtient en ajoutant n+1 fois le nombre de bijections d'un ensemble avec seuleument un element en moins, soit avec n elements.
En partant de cette idée:
Regardons un ensemble a n+1 element, et n'en choisissons que n définis parmis ces n+1 dans l'ensemble de depart et n autre dans l'ensemble d'arrivée.
Il y aura n! bijections differentes a partir de ces deux familles de n elements.
Maintenant construisons a partir de ces bijections de sous ensembles a n elements choisis, l'ensemble des bijections a n+1 elements.
Excluons de maniere definitive le premier element de l'ensemble de depart(je dis premier pour le differencier, cela ne veut evidemment pas dire que j'induis une relation d'ordre). C'est a partir de lui que nous allons construire les bijections a n+1 element.
Associons le a un element de l'ensemble d'arrivée.
Associons les n elements de depart restant de facon a former une bijection avec les autres elements de l'ensemble d'arrivée, ce sous ensemble a n element a donc n! bijection differente et au final nous avons compter toutes les bijections a n+1 elements ou le premier elements etait associé au premier. Il y en a n!
Faisons exactement la meme methode mais en associant le premier element, (c'est toujours le meme qu'on exclu) , au deuxieme element par exemple de l'ensemble d'arrivée. Associons les n elements de depart restant de facon a former une bjection avec les autres elements de l'ensemble d'arrivée, ce sous ensemble a n element a donc n! bijections differentes et au final nous avons compter toutes les bijections a n+1 elements ou le premier elements etait associé au deuxieme elements cette fois.
Faisons pareille n+1 fois en associant a chaque fois le premier element au nieme element de l'ensemble d'arrivée.
Au final nous formons toute les bijections possibles, simplement en sommant l'ensemble des bijections possibles une fois que cet element est associé a un l'element particulier de l'ensemble d'arrivée. On fait cela n+1 fois pour les n+1 elements,on compte donc n+1 fois le nombre de bijection d'un ensemble a n element soit (n+1)*n!. Et on trouve bien que le nombre de bijection d'un ensemble a n+1 element est egal a n+1 fois le nombre de bijections d'un ensemble a n elements.
Mais si l'on omet d'associer un element au premier element que l'on a exclu, disons lui meme. On ne va pas le faire n+1 fois mais n fois.
On a ainsi construit le dernier element de la somme des kk! c'est a dire n*n!.
Il nous reste maintenant a compter toute les bijections ou le premier element est associé au premier pour reconstituer la somme des bijections d'un ensemble a n+1 elements.
On recommence le meme procedé avec le deuxieme element(qui donc ne peut etre associé au premier, tout comme les n-1 autres elements en bijections).
Mais, cette fois, on aura a le faire avec n-1 elements en bijection parmis les n+1 car le premier est deja associé au premier et le deuxieme est celui que l'on fixe a un element de l'ensemble d'arrivée a chaque fois.
Au final on fait cela n fois, et l'on construit l'ensemble des bijection a n+1 element en sommant:
n*n!(ce qu'on a trouvé avant) + n*(n-1)!(ce qu'on vient de trouver)
Mais, si une nouvelle fois on ommet d'associer un element a ce deuxieme element que l'on a exclu et qui nous sert de parametre, disons lui meme on ne fait la somme que (n-1 fois) et donc on a construit l'avant dernier element de la somme qui vaut (n-1)*(n-1)!:
Il nous reste maintenant a compter toute les bijections ou le premier element est associé au premier et le deuxieme au deuxieme.
On recommence alors avec le troisieme elements...
On fait ainsi le meme procédé jusqu'a n'avoir plus que trois elements a associer, on fixe donc l'antepenultieme element et on compte(les n-2 autres elements ont deja leur image définie et fixé):
on fixe l'antepenultieme element:
il reste 2! bijection avec les deux autres et on fait cela 2 fois:
donc 2*2.
On garde le cas ou il est associé a lui meme:
on recommence et cela donne avec l'avant dernier 1*1.
C'est a dire le cas ou il n'est pas associé a lui meme.
Et la somme a ce stade est constituée.
Mais il manque donc pour former l'ensemble des bijections a n+1 elements le cas ou il est associé a lui meme et ou tout les autres sont aussi associés a eux meme(puisque a ce niveau tout les autres elements ont une image attribuée qui est eux meme d'apres notre construction), nous avons donc compter toute les bijections sauf l'identité, c'est a dire que:
Il ne reste donc plus qu'a rajouter 1 cas.
donc au final:
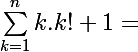
nombre de bijections d'un ensemble a n+1 elements
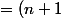!)
.
et donc
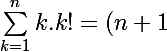! - 1)
Soit si
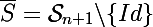
avec Sn l'ensemble des bijections d'un ensemble a n elements dans lui meme, alors
 = \Large \sum\limits_{k=1}^n k.k! =\Large (n+1)!-1)
.
En fait la somme
 = \Large \sum\limits_{k=1}^n k.k!)
.
Compte toute les bijections d'un ensemble a n+1 elements sauf une.
On peut choisir l'identité ou n'importe quelle autre bijection, cette bijection depend juste de l'element que l'on a attribué a chaque elements respectifs, a chaque etape, au cours de la sommation.
. Cette formule se montre très facilement* mais je cherchais une interprétation combinatoire.
, alors
, car c'est le nombre de permutations d'un ensemble à n+1 éléments privées de l'identité. Je cherche à interpréter
, je veux dire par là que je cherche une façon de dénombrer
qui se reflète dans la somme. Bien sûr, j'ai pensé qu'on prenait un élément parmi k et on regardait les permutations de k éléments. Mais je ne vois pas pourquoi ça dénombre
...
, c'est l'ensemble des bijections des ensembles à n+1 éléments, mais je n'arrive pas à faire le S gothique...
