Décomposition d'une fonction continue

[Nightmare]

Bonjour à tous :happy3:

Voici une question que je me suis posé dont je n'ai pas la réponse

Peut-on toujours écrire une fonction continue comme somme d'une fonction croissante et d'une fonction décroissante?

D'un côté on se dit "pourquoi pas", de l'autre on regarde la fonction horrible de Weirstrass et on se dit que ça semble difficile.

Je me pose la même question avec convexe (resp. concave) à la place de croissante (resp. décroissante).

Une idée?

Merci :happy3:

[leon1789]

Salut,

Tu veux que les fonctions monotones soient continues aussi, ou pas forcément ?

[Nightmare]

Pas forcément.

[ThSQ]

Peut-on toujours écrire une fonction continue comme somme d'une fonction croissante et d'une fonction décroissante?

Hélas non. Une fonction monotone est dérivable presque partout. La somme de 2 fonctions monotones aussi. Or il existe des fonctions continues dérivables nulle part.

Je me pose la même question avec convexe (resp. concave) à la place de croissante (resp. décroissante).

Là oui :++:

Une fonction concave est localement lipstruc donc localement à variation bornée et donc la différence de 2 fonctions croissantes = fonction croissante + fonction décroissante

http://fr.wikipedia.org/wiki/Fonction_%C3%A0_variation_born%C3%A9e

Edit : euh, zut, j'ai mal lu. J'ai cru que la question était "Peut-on toujours écrire une fonction convexe comme ...."

On peut encore moins toujours écrire une fonction continue comme somme de fonctions convexes ou concaves

[Nightmare]

merci ThSQ de ta réponse :happy3: Ce n'était pas si dur que ça :lol3:

Pour la 2nd je me suis mal fait comprendre, je voulais savoir si on pouvait décomposer une fonction continue comme somme d'une fonction convexe et d'une fonction concave.

:happy3:

[Nightmare]

Cela dit la réponse est donc aussi non puisqu'une fonction convexe est dérivable sauf sur un ensemble dénombrable.

[ThSQ]

Oui j'avais lu trop vite, sorry.

[ThSQ]

Tiens, Je viens de penser à ça (ça m'a l'air juste) :

Soit f, IR+->IR, suffisamment régulière (continue, monotone, ...).

1- Montrer qu'il existe g croissante et h décroissante telles que h(x) <= f(x) <= g(x). (bon, facile ...)

2- Montrer qu'on peut prendre g et h

[leon1789]

[quote="ThSQ"]
1- Montrer qu'il existe g croissante et h décroissante telles que h(x) > qui donne !!![/B]

[raito123]

(...)

Tiens , il y a un bug dans le forum sur > qui donne !!!

Y a aussi > qui donne

[Antho07]

jolie bug en effet

[ThSQ]

si f n'est pas minorée en - infini

Oui c'est pour ça que j'ai mis : f : IR+ -> IR

[leon1789]

Oui c'est pour ça que j'ai mis : f : IR+ -> IR

Ah oui, je n'avais pas vu :we:

Avec une fonction f bornée sur tout compact,


Après, il suffit de lisser en dessous de h (resp. au dessus de g).

[ThSQ]

Après, il suffit ..

Oui, bon ....

[leon1789]

Pour h par exemple (g fonctionne en symétrique),
le problème revient à interpoler les points , , , etc., de manière décroissante et . Pas de problème avec des trucs du style .

[ThSQ]

.

C'était mon idée aussi.

Ceci dit si on voit bien ce qu'il faut faire, c'est pas aussi simple qu'une interpolation lissée de manière C°° (faut prouver qu'on recoupe pas f par inadvertance !)

[leon1789]

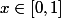
oui, c'est exact, d'où l'intérêt de travailler avec en "décalage constant" (de 1 par exemple) : pour , on a ,
autrement dit