Salut !
merci puor votre réponse ..
En fait je dois calculer (je m'aide de Matlab) un algo de validation croisée généralisée..
En input j'ai une matrice S de taille

, une matrice Q de taille

, et un vecteur y de taille

.
Normalement les trois premières étapes de l'algo sont :
(a) Calculer la decomposition QR de S, tel que
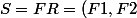(R1\,0)^T)
(j'ai mis transpose parce que normalement c'est à la verticale ..)
(b) Calculer
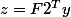
et
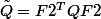
(c) Calculer
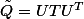
où U est orthogonale et T tridiagonale ...
voila ...normalement d'après ce que j'ai compris, dans l'étape (a) la matrice F2 n'est nécéssairement pas carrée, parce que R1 est carrée. Ebnfin je l'ai compris comme ça d'où le fait d'avoir une matrice Q non carrée ??
merci encore et par avance

))))
