Décomposer en éléments simple sur C et sur R la fraction rationnelle
X²+X+1/X^4+1
Merci de m'aider je ne sais pas comment m'y prendre.
Décomposition de fractions rationelles
11 messages
- Page 1 sur 1
par mathelot » 19 Oct 2014, 15:51
bonjour,
d'après le cours, c'est de la forme
=\frac{a_1}{x-e^{\frac{i\pi}{4}}}+\frac{a_2}{x-e^{\frac{i3\pi}{4}}} +\frac{a_3}{x-e^{\frac{5i\pi}{4}}}+\frac{a_4}{x-e^{\frac{7i\pi}{4}}})
où les dénominateurs s'annulent pour les racines 4ème de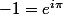
.
et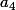 
sont conjuguées ainsi que 
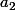et 
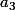
faire tendre x vers l'infini donne une relation
en x=0, une seconde relation
éventuellement multiplier des deux côtés par
l'égalité et faire tendre x vers 
où est un pôle (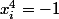
)
d'après le cours, c'est de la forme
où les dénominateurs s'annulent pour les racines 4ème de
faire tendre x vers l'infini donne une relation
en x=0, une seconde relation
éventuellement multiplier des deux côtés par
où
par methammer » 19 Oct 2014, 16:27
pourrais tu m'expliquer plus en détail la détermination des constantes s.t.p.
par chan79 » 19 Oct 2014, 18:54
approche plus basique (la méthode de mathelot est meilleure)
(x^2+i)}=\fra{x^2+x+1}{(x-a)(x+a)(x-b)(x+b)}=\fra{m}{x-a}+\fra{n}{x+a}+\fra{p}{x-b}+\fra{q}{x+b})
avec
donc 
et
donc 
on réduit au même dénominateur l'expression à la fin de la première ligne et on identifie les coefficients avec l'expression précédente, en laissant a et b pour les calculs
on trouve
(x(m+n)+a(m-n))+(x^2-i)(x(p+q)+b(p-q))=x^2+x+1)
+b(p-q)=1)
-i(p+q)=1)
-ib(p-q)=1)
il y a du calcul mais ça se fait bien
}{4(x-\fra{1+i}{\sqrt{2}})}+\fra{-i(1-\sqrt{2})}{4(x+\fra{1+i}{\sqrt{2}})}+\fra{i(1+ \sqrt{2} )}{4(x-\fra{1-i}{\sqrt{2}})}+\fra{i(1-\sqrt{2})}{4(x+\fra{1-i}{\sqrt{2}})})
avec
et
on réduit au même dénominateur l'expression à la fin de la première ligne et on identifie les coefficients avec l'expression précédente, en laissant a et b pour les calculs
on trouve
il y a du calcul mais ça se fait bien
par chan79 » 20 Oct 2014, 10:26
methammer a écrit:Décomposer en éléments simple sur C et sur R la fraction rationnelle
X²+X+1/X^4+1
Merci de m'aider je ne sais pas comment m'y prendre.
pour décomposer sur
par Ben314 » 20 Oct 2014, 11:59
C'est effectivement une "très jolie astuce", mais à mon avis, c'est plus pédagogique de commencer par écrire la décomposition en facteurs irréductibles sur C[X] (qui se déduit directement du cours sur les racines n-ièmes dans C) puis d'en déduire celle sur R[X] par regroupement deux par deux des facteurs correspondants à des racines conjuguées.chan79 a écrit:pour décomposer sur, remarquer que:
(on obtient bien évidement le même résultat...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 20 Oct 2014, 12:06
RAPPEL (@methammer) tu as du voir au collège... que les multiplications-divisions sont prioritaires sur les additions-soustractions.
Donc ça :
... 
Donc ça :
Il n'y a qu'une et une seule façon de l'interpréter, à savoirmethammer a écrit:X²+X+1/X^4+1
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :