Bonjour,
Je dois décomposer la fraction suivante en élément simple dans R(X) :
F(X)=8X/(X²-1)^3
Si quelqu'un peut m'aider
Décomposition fraction rationnelle
12 messages
- Page 1 sur 1
Re: décomposition fraction rationnelle
Bonsoir
Commence par lire un cours sur la décomposition en éléments simples ...
Il y en a plein sur internet.
Commence par lire un cours sur la décomposition en éléments simples ...
Il y en a plein sur internet.
Re: décomposition fraction rationnelle
Bonjour,
Un petit coup de pouce pour débuter, peut être :
on décompose x^2 - 1 en produit de polynômes irréductibles :
x^2 - 1 =(x-1).(x+1)
ainsi
f(x) = 8x / ( (x-1)^3.(x+1)^3 )
Puis on observe que f est impaire :
pour tout x de R-{-1,1}
f(-x) = -f(x)
ce qui simplifie beaucoup la recherche
http://gchagny.perso.math.cnrs.fr/Fract ... lesDES.pdf
voir 2.3.3 et 2.3.4
Proposez vos essais
Un petit coup de pouce pour débuter, peut être :
on décompose x^2 - 1 en produit de polynômes irréductibles :
x^2 - 1 =(x-1).(x+1)
ainsi
f(x) = 8x / ( (x-1)^3.(x+1)^3 )
Puis on observe que f est impaire :
pour tout x de R-{-1,1}
f(-x) = -f(x)
ce qui simplifie beaucoup la recherche
http://gchagny.perso.math.cnrs.fr/Fract ... lesDES.pdf
voir 2.3.3 et 2.3.4
Proposez vos essais
Re: décomposition fraction rationnelle
Voila ce que j'ai pour l'instant
8x/〖(x^2-1)〗^3 = a/〖(x-1)〗^3 + b/〖(x-1)〗^2 + c/〖(x-1)〗^1 + d/〖(x+1)〗^3 + e/〖(x+1)〗^2 + f/〖(x+1)〗^1
-F(X) =- a/〖(x-1)〗^3 - b/〖(x-1)〗^2 - c/〖(x-1)〗^1 - d/〖(x+1)〗^3 - e/〖(x+1)〗^2 - f/〖(x+1)〗^1
F(-X) = a/〖(-x-1)〗^3 + b/〖(-x-1)〗^2 + c/〖(-x-1)〗^1 + d/〖(-x+1)〗^3 + e/〖(-x+1)〗^2 + f/〖(-x+1)〗^1
Par identification f=c ; e=-b et a=d
En multipliant par 〖(x^2-1)〗^(3 )on sort a = d = 1
8x/〖(x^2-1)〗^3 = 1/〖(x-1)〗^3 + b/〖(x-1)〗^2 + c/〖(x-1)〗^1 + 1/〖(x+1)〗^3 + (-b)/〖(x+1)〗^2 + (-c)/〖(x+1)〗^1
ensuite je bloque pour b et c. le passage a la limite ne m'aide pas
8x/〖(x^2-1)〗^3 = a/〖(x-1)〗^3 + b/〖(x-1)〗^2 + c/〖(x-1)〗^1 + d/〖(x+1)〗^3 + e/〖(x+1)〗^2 + f/〖(x+1)〗^1
-F(X) =- a/〖(x-1)〗^3 - b/〖(x-1)〗^2 - c/〖(x-1)〗^1 - d/〖(x+1)〗^3 - e/〖(x+1)〗^2 - f/〖(x+1)〗^1
F(-X) = a/〖(-x-1)〗^3 + b/〖(-x-1)〗^2 + c/〖(-x-1)〗^1 + d/〖(-x+1)〗^3 + e/〖(-x+1)〗^2 + f/〖(-x+1)〗^1
Par identification f=c ; e=-b et a=d
En multipliant par 〖(x^2-1)〗^(3 )on sort a = d = 1
8x/〖(x^2-1)〗^3 = 1/〖(x-1)〗^3 + b/〖(x-1)〗^2 + c/〖(x-1)〗^1 + 1/〖(x+1)〗^3 + (-b)/〖(x+1)〗^2 + (-c)/〖(x+1)〗^1
ensuite je bloque pour b et c. le passage a la limite ne m'aide pas
Re: décomposition fraction rationnelle
Je vais vous répondre en détail, pour le moment rectifiez une erreur : à la fin f=c et non -c
Re: décomposition fraction rationnelle
f=c et non -c , à rectifier dans la dernière égalité ,
et un détail : (x-1)^1 pourra s'écrire (x-1) sans inconvénient , de même bien sûr pour (x+1).
Une remarque : on part de P(x)/Q(x) avec deg(P) <deg(Q), ce qui justifie l'écriture de début.
Ensuite étudiez lim( x.f(x) ) lorsque x tend vers +infini : cela vous permet de conclure c=0,
Il ne reste plus que b : posez x=2 pour conclure.
a=1 est exact mais me semble être à justifier davantage
A vous
et un détail : (x-1)^1 pourra s'écrire (x-1) sans inconvénient , de même bien sûr pour (x+1).
Une remarque : on part de P(x)/Q(x) avec deg(P) <deg(Q), ce qui justifie l'écriture de début.
Ensuite étudiez lim( x.f(x) ) lorsque x tend vers +infini : cela vous permet de conclure c=0,
Il ne reste plus que b : posez x=2 pour conclure.
a=1 est exact mais me semble être à justifier davantage
A vous
Re: décomposition fraction rationnelle
Désolé, erreur de frappe et de copier coller.
Je trouve b = -0.5 en faisant le calcul.
Lim xF(x) = 8x²/〖(x^2-1)〗^3 du type 1/x^4 = 0 quand x -> ∞ et donc c = 0.
du coup :
F(X) = 1/〖(x-1)〗^3 + (-1)/〖2(x-1)〗^2 + 1/〖(x+1)〗^3 + 1/〖2(x+1)〗^2
Est-ce exact ?
Je trouve b = -0.5 en faisant le calcul.
Lim xF(x) = 8x²/〖(x^2-1)〗^3 du type 1/x^4 = 0 quand x -> ∞ et donc c = 0.
du coup :
F(X) = 1/〖(x-1)〗^3 + (-1)/〖2(x-1)〗^2 + 1/〖(x+1)〗^3 + 1/〖2(x+1)〗^2
Est-ce exact ?
Re: décomposition fraction rationnelle
Oui et non, disons que c'est un premier brouillon :
il est indispensable de commencer par prouver c = o AVANT de calculer b
(sinon pour x=2, on a toujours un terme c+c/3 et il faut une autre relation...)
Essayez de mieux justifier lim(x.f(x))=0 quand x -> +∞ :
« du type 1/x^4 » c'est l'idée générale...
et il faut aussi se préoccuper du terme de droite : quelle est sa limite ?
Pour b il faut présenter au moins la première ligne du calcul, pour s'expliquer un peu
Et, à nouveau, il faut en faire plus pour annoncer a=1
Il y a eu des erreurs de copier coller dans le résultat , des « 2 » ont dérapé :
f(x) = 1/(x-1)^3 – (1/2)/(x-1)^2 + 1/(x+1)^3 + (1/2)/(x+1)^2
il est indispensable de commencer par prouver c = o AVANT de calculer b
(sinon pour x=2, on a toujours un terme c+c/3 et il faut une autre relation...)
Essayez de mieux justifier lim(x.f(x))=0 quand x -> +∞ :
« du type 1/x^4 » c'est l'idée générale...
et il faut aussi se préoccuper du terme de droite : quelle est sa limite ?
Pour b il faut présenter au moins la première ligne du calcul, pour s'expliquer un peu
Et, à nouveau, il faut en faire plus pour annoncer a=1
Il y a eu des erreurs de copier coller dans le résultat , des « 2 » ont dérapé :
f(x) = 1/(x-1)^3 – (1/2)/(x-1)^2 + 1/(x+1)^3 + (1/2)/(x+1)^2
Re: décomposition fraction rationnelle
oui bien sur les 2 sont en-dehors des parenthèses.
Ayant fini mes études depuis longtemps, je ne me suis pas attardé sur les calculs car je voulais surtout avoir la méthode de résolution (qui n'était pas dans mes cours).
Merci en tout cas pour votre aide et bonne continuation.
Ayant fini mes études depuis longtemps, je ne me suis pas attardé sur les calculs car je voulais surtout avoir la méthode de résolution (qui n'était pas dans mes cours).
Merci en tout cas pour votre aide et bonne continuation.
Re: décomposition fraction rationnelle
Bonjour,
Une variante. Ici, le pôle 1 de la fraction rationnelle est d'ordre 3, ce qui est assez élevé.
Pour calculer la partie polaire relative à un pôle de la fraction rationnelle d'ordre élevé, il peut être commode d'utiliser la division suivant les puissances croissantes.
En posant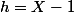 , la fraction rationnelle devient
, la fraction rationnelle devient ^3}) . On fait alors la division suivant les puissances croissantes de
. On fait alors la division suivant les puissances croissantes de  par
par ^3=8+12h+6h^2+h^3) à l'ordre 2 :
à l'ordre 2 : 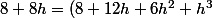\times (1-(1/2)h +0\,h^2) +h^3(\text{quelque chose polynomial en } h)) .
.
En divisant le quotienth +0\,h^2) par
par 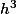 et en rétablissant
et en rétablissant 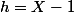 , on obtient la partie polaire relative au pôle 1 :
, on obtient la partie polaire relative au pôle 1 : ^3}-\dfrac1{2(X-1)^2}+\dfrac0{X-1}) .
.
Une variante. Ici, le pôle 1 de la fraction rationnelle est d'ordre 3, ce qui est assez élevé.
Pour calculer la partie polaire relative à un pôle de la fraction rationnelle d'ordre élevé, il peut être commode d'utiliser la division suivant les puissances croissantes.
En posant
En divisant le quotient
Re: décomposition fraction rationnelle
@GaBuZoMeu
Nos messages se sont croisés
avec les deux méthodes rebeldelaforai a, à présent, une révision complète sur ce thème
Nos messages se sont croisés
avec les deux méthodes rebeldelaforai a, à présent, une révision complète sur ce thème
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
