Décomposition en élement simple
15 messages
- Page 1 sur 1
Décomposition en élement simple
Bonjour!
Pourriez vous m'aider a effectuer la décomposition en élément simple de la fonction suivante:
1/(x²-a)² avec a: une constante.
Je vous remerci d'avance pour vos réponses!
Pourriez vous m'aider a effectuer la décomposition en élément simple de la fonction suivante:
1/(x²-a)² avec a: une constante.
Je vous remerci d'avance pour vos réponses!
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
(Correction : l'intégrale donnée dans l'autre discussion n'est pas celle que j'ai écrit plus bas. Je suis une buse.)
Lfanny : s'il s'agit de calculer l'intégrale donnée dans l'autre discussion, à savoir , je préfère une méthode beaucoup plus simple : poser t = 1/x (c'est le premier changement de variable qui me vient à l'esprit, pas toi ? - oui, ou bien on peut faire t = b/x, c'est pareil). On obtient, si je ne dis pas de bêtise :
, je préfère une méthode beaucoup plus simple : poser t = 1/x (c'est le premier changement de variable qui me vient à l'esprit, pas toi ? - oui, ou bien on peut faire t = b/x, c'est pareil). On obtient, si je ne dis pas de bêtise :
} = \int_{1/s}^{1/r} \frac{dt}{t^2(a+bt)})
dont la fraction rationnelle est bien plus simple à décomposer (on peut même se passer de la théorie de la décomposition en éléments simples).
-------------------------------
Sinon, pour info (parce que, bêtement, j'avais commencé par regarder la décomposition du premier message (correction : ce qui n'était pas si bête que ça en fin de compte)), pour décomposer une fraction rationnelle en éléments simples, il y a deux étapes (dans le cas général) : 1. écrire la décomposition a priori, 2. calculer les coefficients.
Voici la décomposition a priori (en supposant a positif, sinon il n'y a rien à décomposer) :
^2(x+\sqrt{a})^2}=\frac{A}{x-\sqrt{a}}+\frac{B}{(x-\sqrt{a})^2}<br />+\frac{C}{x+\sqrt{a}}+\frac{D}{(x+\sqrt{a})^2})
Pour trouver B on multiplie les deux membres par^2) et on pose
et on pose 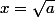 . Même méthode pour trouver D.
. Même méthode pour trouver D.
(Escargot92 :^2\, f(x)) ne fait pas 0 car - et c'est fait exprès ! - le facteur
ne fait pas 0 car - et c'est fait exprès ! - le facteur ^2) se simplifie avec celui du dénominateur...)
se simplifie avec celui du dénominateur...)
Pour trouver A et C on utilise deux valeurs particulières, par exemple on pose x=0 et on regarde ce qui se passe, ça donne une première relation entre A et C, puis on multiplie par x et on fait tendre x vers l'infini (de façon à faire ressortir A et C) pour avoir une deuxième relation.
Bref, ce sont les méthodes habituelles.
Si on ne connaît pas ces méthodes, il y a la méthode "bourrin", longue mais qui marche toujours : mettre tout le membre de droite au même dénominateur et identifier les deux numérateurs (ce sont des polynômes donc ils ont les mêmes coefficients).
PS : j'ai trouvé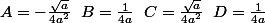 (en espérant ne pas m'être trompé...)
(en espérant ne pas m'être trompé...)
Lfanny : s'il s'agit de calculer l'intégrale donnée dans l'autre discussion, à savoir
dont la fraction rationnelle est bien plus simple à décomposer (on peut même se passer de la théorie de la décomposition en éléments simples).
-------------------------------
Sinon, pour info (parce que, bêtement, j'avais commencé par regarder la décomposition du premier message (correction : ce qui n'était pas si bête que ça en fin de compte)), pour décomposer une fraction rationnelle en éléments simples, il y a deux étapes (dans le cas général) : 1. écrire la décomposition a priori, 2. calculer les coefficients.
Voici la décomposition a priori (en supposant a positif, sinon il n'y a rien à décomposer) :
Pour trouver B on multiplie les deux membres par
(Escargot92 :
Pour trouver A et C on utilise deux valeurs particulières, par exemple on pose x=0 et on regarde ce qui se passe, ça donne une première relation entre A et C, puis on multiplie par x et on fait tendre x vers l'infini (de façon à faire ressortir A et C) pour avoir une deuxième relation.
Bref, ce sont les méthodes habituelles.
Si on ne connaît pas ces méthodes, il y a la méthode "bourrin", longue mais qui marche toujours : mettre tout le membre de droite au même dénominateur et identifier les deux numérateurs (ce sont des polynômes donc ils ont les mêmes coefficients).
PS : j'ai trouvé
Robic a écrit:Lfanny : s'il s'agit de calculer l'intégrale donnée dans l'autre discussion, à savoir, je préfère une méthode beaucoup plus simple : poser t = 1/x (c'est le premier changement de variable qui me vient à l'esprit, pas toi ? - oui, ou bien on peut faire t = b/x, c'est pareil). On obtient, si je ne dis pas de bêtise :
dont la fraction rationnelle est bien plus simple à décomposer (on peut même se passer de la théorie de la décomposition en éléments simples).
encore plus simple ::
:zen:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
