Decomposition dans R(X) et C(X)

par **victen** » 30 Oct 2013, 13:36

Bonjour, on me demande de décomposer des polynômes dans R(X) et C(X)

Je suis tombé sur un polynôme sans racines evidentes, je n'arrive pas à le decomposer

X^9-X^3+1

J'ai voulu commencé par poser Y=X^3 et donc Y^3-Y+1 ...

Merci de votre aide :help:

par **arnaud32** » 30 Oct 2013, 13:51

tu peux utiliser ca: http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan

par **chan79** » 30 Oct 2013, 13:53

victen a écrit:Bonjour, on me demande de décomposer des polynômes dans R(X) et C(X)

Je suis tombé sur un polynôme sans racines evidentes, je n'arrive pas à le decomposer

X^9-X^3+1

J'ai voulu commencé par poser Y=X^3 et donc Y^3-Y+1 ...

Merci de votre aide :help:

il y aurait bien la méthode de Cardan, avec du calcul ....

par **victen** » 30 Oct 2013, 13:54

Oui mais ne l'ayant pas vu en cours je ne pense pas que cela soit la bonne solution pour le moment.. Même si elle conviendrait !

par **Ben314** » 30 Oct 2013, 13:54

Pour les polynômes de degrés 3, il y a des formules (dites "de cardan") qui permettent de déterminer les racines, mais ces formules sont rarement enseignées vu leur peu d'utilité "numérique".
Selon wolfram, la factorisation est : http://www.wolframalpha.com/input/?i=X%5E3-X%2B1
(et on ne peut pas la trouver sans savoir résoudre les équations du 3em degré)

Donc PERSONELLEMENT, j'aurais tendance à penser à une faute de frappe dans l'énoncé (ou a une erreur de calcul si ton fameux X^9-X^3+1 est issu d'un calcul et pas directement de l'énoncé)

par **victen** » 30 Oct 2013, 13:59

Ah non non c'est tiré d'un exercice ou il est juste demandé de "Décomposer dans R(X) et C(X) le polynôme suivant : X^9-X^3+1

par **chan79** » 30 Oct 2013, 14:24

victen a écrit:Ah non non c'est tiré d'un exercice ou il est juste demandé de "Décomposer dans R(X) et C(X) le polynôme suivant : X^9-X^3+1

c'est quand même une erreur, je pense
Regarde la tête de l'unique solution réelle:

par **victen** » 30 Oct 2013, 14:28

En effet ...
Peut être alors de l'aide sur la decomposition de (X+1)^6-X^6 ?

(X+1)^6-X^6 = ((X+1)^3)^2-(X^3)^2

= ((X+1)^3-X^3)((X+1)^3+X^3)

= (((X+1)-X)((X+1)^2+(X+1)X+X^2)))((X+1)+X)((X+1)^2-((X+1-X+X^2) => decomposition dans R(X) ??

par **chan79** » 30 Oct 2013, 14:41

victen a écrit:En effet ...
Peut être alors de l'aide sur la decomposition de (X+1)^6-X^6 ?

(X+1)^6-X^6 = ((X+1)^3)^2-(X^3)^2

= ((X+1)^3-X^3)((X+1)^3+X^3)

= (((X+1)-X)((X+1)^2+(X+1)X+X^2)))((X+1)+X)((X+1)^2-((X+1-X+X^2) => decomposition dans R(X) ??

tu devrais mettre l'énoncé original

par **victen** » 30 Oct 2013, 14:43

Decomposer en facteurs irreductibles les polynômes suivants :

P=X^9-X^3+1
P=(X+1)^6-X^6

par **arnaud32** » 30 Oct 2013, 14:43

ssi

tu poses

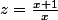
... tu auras tes solutions dans C

sinon

par **victen** » 30 Oct 2013, 14:53

(X+1)^6-X^6 = (3X^2+3X+1)(2X^3+3X^2+3X+1) est la DES dans R(X) ?

par **arnaud32** » 30 Oct 2013, 15:46

quele st le discriminent du premier terme?
les second a forcement une raine reelle (-1/2 par ex) ...

par **chan79** » 30 Oct 2013, 17:55

arnaud32 a écrit:quele st le discriminent du premier terme?
les second a forcement une raine reelle (-1/2 par ex) ...

salut
si on sait, par un moyen ou un autre que -1/2 est solution ...
2x³+3x²+3x+1=2x³+x²+2x²+x+2x+1=x²(2x+1)+x(2x+1)+(2x+1)=(2x+1)(x²+x+1)

par **victen** » 30 Oct 2013, 19:22

Le discrimant du premier terme est négatif (Delta=9-12=-3), il y a donc une racine complexe!
Pour la decomposition dans R(X) m'arrêter à (3x²+3x+1)(2x+1)(x²+x+1) est-ce juste ?

par **chan79** » 30 Oct 2013, 19:59

victen a écrit:Le discrimant du premier terme est négatif (Delta=9-12=-3), il y a donc une racine complexe!
Pour la decomposition dans R(X) m'arrêter à (3x²+3x+1)(2x+1)(x²+x+1) est-ce juste ?

il y a deux racines complexes
dans R(X), c'est bon

par **victen** » 30 Oct 2013, 20:26

D'accord

Oui dans C(X) j'ai la racine de (3X²+3X+1) et de (X²+X+1)

je trouve pour 3X²+3X+1 :
x1=(-3+iV3)/6
x2=(-3-iV3)/6

et pour X²+X+1 les racines sont j et j^2 !

par **chan79** » 30 Oct 2013, 21:03

pour

on a une solution en écrivant que x+1 et x sont opposés

par **victen** » 30 Oct 2013, 21:07

Je vois pas là ou vous voulez en venir..

par **chan79** » 31 Oct 2013, 07:10

victen a écrit:Je vois pas là ou vous voulez en venir..

c'est simplement qu'on a une solution de

en résolvant x+1=-x
donc (2x+1) est un facteur dans la décomposition de

Decomposition dans R(X) et C(X)

Decomposition dans R(X) et C(X)

Qui est en ligne