Curiosité

par **fahr451** » 03 Juin 2007, 10:59

bonjour à tous

pas un défi mais un tit résultat simple , que je ne connaissais pas .

A,B deux éléments de Mn(C) vérifiant AB = 0
montrer qu'elles sont simultanément "trigonalisables"

par **fahr451** » 04 Juin 2007, 16:16

je fais remonter ce résultat qui m'avait bien plu et qui n' a pas encore rencontré son public.

par **aviateurpilot** » 04 Juin 2007, 16:21

fahr451 a écrit:je fais remonter ce résultat qui m'avait bien plu et qui n' a pas encore rencontré son public.

c'est quoi une matrice "trigonalisables" stp

par **yos** » 04 Juin 2007, 16:40

fahr451 a écrit:...ce résultat n' a pas encore rencontré son public.

Ben moi j'ai déjà trouvé la réciproque.

par **SimonB** » 04 Juin 2007, 16:44

Une matrice trigonalisable dans Mn(K), aviateurpilot, est une matrice qui peut s'écrire sous la forme P^-1*T*P, où P est dans GLn(K), et où T est triangulaire supérieure.

Et on dit de deux matrices qu'elles sont simultanément trigonalisables, si les endomorphismes associés trigonalisent dans une même base, id est si elles ont même matrice de passage P.

Oui, sans ça, c'est du cours de spé, ce résultat... Mais la démonstration est jolie.

par **Lierre Aeripz** » 04 Juin 2007, 16:58

C'est compliqué à écrire en Latex les matrices par bloc... Je crois que j'ai vraiment trop la flemme... :)

par **fahr451** » 04 Juin 2007, 19:03

SimonB a écrit:.

Oui, sans ça, c'est du cours de spé, ce résultat... Mais la démonstration est jolie.

on fait beaucoup de choses en spé finalement

par **yos** » 04 Juin 2007, 19:15

fahr451 a écrit:on fait beaucoup de choses en spé finalement

On fait même des drapeaux! Sais-tu ce qu'est un drapeau Fahr?

par **fahr451** » 04 Juin 2007, 19:20

un mot savant pour un truc très simple oui j'ai bien dû m 'y mettre

par **yos** » 04 Juin 2007, 19:24

Ben oui c'est une suite strictement croissante de n+1 sev. J'ai vu ça pour la première fois dans les programmes de spé de 95.
Donc pour en revenir à l'exo, il nous faut un drapeau qui soit A-stable et B-stable. Ce genre de chose se fabrique par récurrence.

par **fahr451** » 04 Juin 2007, 19:26

oui mais comme toute récurrence faut démarrer l'usine à gaz

par **SimonB** » 04 Juin 2007, 22:00

Bon, en fait, c'est peut-être de l' "adhérence" de cours de spé, ça. Tout comme les drapeaux d'ailleurs (je ne connais que peu de gens en spé qui ne l'ont pas vu, mais généralement en DM)...

par **fahr451** » 04 Juin 2007, 22:03

et si tu donnais le point clé puisque c'est si classique

par **SimonB** » 04 Juin 2007, 22:21

Comme yos l'a dit, on procède par récurrence, et pour passer au rang (n+1) on décompose par blocs de tailles 1 et n. Le point clef étant que A et B possèdent un vecteur propre commun puisqu'elles commutent...

par **fahr451** » 04 Juin 2007, 22:22

elles commutent ?

par **SimonB** » 04 Juin 2007, 22:24

Ooooooops, je me suis planté dans la relecture de l'énoncé. Il est tard et temps d'aller me coucher... Excusez-moi (il me semble cela dit que le résultat est quand même dans mon cours, mais là je n'ai plus la démonstration dans la tête ! ;) ) :hum:

par **fahr451** » 04 Juin 2007, 22:30

alors pour autant que je sache

il est classique (et connu des taupins)que deux matrices qui commutent sont simultanément trigonalisables
le résultat ici fort proche l'est beaucoup moins
la preuve étant très proche ; seul le commencement demande un chouia de plus

par **Daniel-Jackson** » 05 Juin 2007, 19:55

fahr451 a écrit:alors pour autant que je sache

il est classique (et connu des taupins)que deux matrices qui commutent sont simultanément trigonalisables
le résultat ici fort proche l'est beaucoup moins
la preuve étant très proche ; seul le commencement demande un chouia de plus

Bon je cherche toujours quand j'ai du temps libre mais je n'ai rien.
Si dans 12 heures à coté de maintenant je ne trouve rien , il me faudra une indication .

Donc top chrono !

par **Daniel-Jackson** » 05 Juin 2007, 21:07

Bon alors j'ai une petite piste :

-Premièrement on écarte les cas triviaux :

Si A (ou ,et B) identiquement nulle.
Si A ( ou strictement B) est inversible ( et on serait au cas précédent)
Si BA = 0 =AB ,au quel cas c'est un résultat classique A et B commuttent

Dans les autres cas , on procède comme pré-suggérer par récurrence:

Comme AB =0 alors immédiatement on tire que

La première conséquence qu'on peut tirer de cette propriété est que tout vecteur propre de B associé à une valeur propore non nulle est dans le Ker(A)

Partant du fait que B est supposé non identiquement nulle , il existe au moins une valeur propre non nulle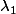

associé au sous espace propre

.
Et on peut écricre C^n comme somme directe de

avec un sous espace H .

La restriction de

qui est inclus dasn Ker(A) est diagonale et A est évidemnt nulle dans

.

En suite j'ai envie de dire que le sous espace H est stable par B !.........mais je suis pas très sûr , comme ça on sait que la restriction de B a H est trigonalisable et en restreignant l'égalité AB=0 dans H , l'hypothèse de récurrence s'applique et on termine ...... (l'hypothèse de récurrence au cas n=1 est plutot facile )

Mais je suis pas sûr de mon coup , je vais encore réfléchir :marteau:

par **Daniel-Jackson** » 05 Juin 2007, 23:30

Oulaaaaaaaaaaaaaaa :briques:
J'ai dit une grosse connerie.

B peut être nilpotente et avoir toutes ses valeur propres nulles .

:stupid_in

Bon je vais aller me coucher :dodo:

Curiosité

curiosité

Qui est en ligne