Cryptographie RSA démontrer une relation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dadoudidou55
 par dadoudidou55 » 17 Mar 2016, 17:13
par dadoudidou55 » 17 Mar 2016, 17:13
Bonjour,
On a deux nombres premiers p et q, soit n le produit p.q.
On a e tel que e est premier avec (p-1)(q-1) et e est inférieur à (p-1)(q-1).
d est l'inverse de e modulo (p-1)(q-1) c'est-à-dire : d.e = 1 mod((p-1)(q-1)).
Le message a crypté est m qui devient c (c=message m crypté).
On sait que :
c = m^e mod(n).
m = c^d mod(n).
Dans l'exercice on a :
d1 = d mod(p-1).
d2 = d mod (q-1).
m1 = c^(d1) mod(p).
m2 = c^(d2) mod(q).
Montrer que :
m = m1 mod(p)
m = m2 mod(q)
On doit utiliser le petit théorème de Fermat et l'exponentiation binaire mais je ne vois pas comment aboutir.
Quelqu'un a-t-il une piste pour m'aider ? Merci

-
Robot
 par Robot » 17 Mar 2016, 17:30
par Robot » 17 Mar 2016, 17:30
C'est quoi l'exponentiation
binaire ?
Il suffit de rappeler l'énoncé du petit théorème de Fermat (pour

par exemple) et de rappeler ce que veut dire
})
pour avoir

.
-
dadouddou55
- Messages: 4
- Enregistré le: 17 Mar 2016, 18:12
-
 par dadouddou55 » 17 Mar 2016, 18:18
par dadouddou55 » 17 Mar 2016, 18:18
Merci de répondre aussi vite. L'exponentiation binaire est le fait de calculer la puissance a en base binaire.
Exemple a=10 et on cherche 3^a = ? mod(n)
10 = 2*5 +0
5 = 2*2+1
2 = 2*1 +0
1 = 2*0 +1
Donc 10 = 2^3 + 2^2
Avec ce résultat il est plus facile de calculer les puissances car il suffit de calculer 2^0 et/ ou 2^1 puis de mettre au carré afin d'avoir les autres puissances mod(n)
d1 = d mod(p-1) signifie qu'il existe un k tel que d=(p-1)k +d1
d1 est le reste de la division euclidienne de d par (p-1) mais je ne sais pas où m'en servir.
Je ne vois pas comment commencer, peux-tu me montrer comment et surtout où utiliser fermat ? Merci
-
Robot
 par Robot » 17 Mar 2016, 21:39
par Robot » 17 Mar 2016, 21:39
Je ne vois pas ce que l'exponentiation rapide viendrait faire ici, dans cette question.
Tu n'as pas écrit l'énoncé du petit théorème de Fermat. Avec
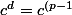k+d_1})
, si tu prends la peine d'énoncer ce théorème pour le nombre premier

, tu devrais voir comment l'utiliser.
-
dadouddou55
- Messages: 4
- Enregistré le: 17 Mar 2016, 18:12
-
 par dadouddou55 » 17 Mar 2016, 22:28
par dadouddou55 » 17 Mar 2016, 22:28
J'ai :
m = c^d [n] = c^((p-1)k) x c^d1 [n].
m1 = c^d1 [n] = c^d x c^((p-1)k) [n].
Mais là je tourne en rond.
Si j'utilise ce que tu m'as dis j'ai :
c^((p-1)k+d1) = c [(p-1)k +d1].
Je pense que je n'ai pas compris ce que tu voulais m'expliquer car après je ne sais pas quoi faire.
Si je décompose j'ai : c^((p-1)k) = c [(p-1)k)]
et c^d1 = c [d1].
Mais avec ça je n'avance pas car les modulo sont différents
-
dadouddou55
- Messages: 4
- Enregistré le: 17 Mar 2016, 18:12
-
 par dadouddou55 » 17 Mar 2016, 22:37
par dadouddou55 » 17 Mar 2016, 22:37
Avec fermat il y a aussi :
c^d = c^((p-1)k) x c^d1.... modulo ??
Et c^((p-1)k) = 1^k [p] = 1 [p].
Mais c^d1 est-t-il défini mod (p) ?
Car dans ce cas je retrouve c^d = c^d1 [p] mais comment justifier le modulo après c^d1 ? Merci
-
dadouddou55
- Messages: 4
- Enregistré le: 17 Mar 2016, 18:12
-
 par dadouddou55 » 17 Mar 2016, 23:51
par dadouddou55 » 17 Mar 2016, 23:51
C'est bon j'ai compris ce qui bloquait.
Donc j'ai c^d = c^d1 [p] et c^d = c^d2 [q].
Mais après je ne vois pas où introduire ces formules

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2016, 07:40
par Ben314 » 18 Mar 2016, 07:40
Salut,
Vu que, par définition, m=c^d mod (n) et que n=pq, on a m=c^d mod (p) et m=c^d mod (q).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
