Croissance Suite

[Fantino]

Bonjour
Soit u(n) avec n appartenant aux naturels non nuls
Si un est croissante prouvez que vn = (u1+u2+u3.... +un) /n est aussi croissante. J'ai vérifié cela avec tous types de suites (stationnaires,un<0....) mais je n'arrive pas à démontrer le cas général sans contraire une expression de un
Merci de votre aide

[Lostounet]

Peut-être regarder le signe de V(n+1)-V(n) ?

[aviateur]

Bonjour,
C'est pas seulement peut être mais c'est sûr qu'il faut faire cela.
Cependant , si j'interviens c'est pas pour ça. Mais simplement pour faire remarquer le côté naturel du résultat.
En effet c'est la moyenne d'une série de nombres (série au sens de la statistique). Si j'ajoute à cette série un nouveau nombre au moins aussi grand que les autres c'est tout à fait naturel de voir la nouvelle moyenne augmenter.

[Fantino]

Merci

[Fantino]

Je me compliquais un peu la vie

[Ben314]

Salut,

Je me compliquais un peu la vie

Vu ta réponse, je me demande si tu as bien compris ce que disait aviateur : ce qu'il dit, c'est que, intuitivement parlant, c'est bien clair que si tes notes aux différents D.S. de maths successifs sont de plus en plus élevées alors ta moyenne en math. est elle aussi en augmentation au cours de l'année.
Sauf que ce "intuitivement" ne constitue pas une preuve mathématique et que donc ce que ton prof. attend, c'est une "vrai preuve" par du calcul en utilisant (par exemple) ce que dit Lostounet.

Et si ça t'amuse, tu peut même démontrer proprement (c'est à dire par du calcul) d'autre résultat eux aussi complètement évidents "intuitivement" parlant :
- Si ta plus mauvaise note est et ta meilleure note est alors ta moyenne est comprise entre et .
- Si pour le moment (avec notes) ta moyenne est de , alors quand tu va avoir une note de plus, ça fera augmenter ta moyenne si (et seulement si) cette nouvelle note est supérieure à la moyenne .

[pascal16]

Vn+1-Vn
= [nUn+1 - somme pour k=1 à n des Uk]/(n(n+1))
= [ somme pour k=1 à n des (Un+1 - Uk) ]/(n(n+1))
= démo finie car somme somme de termes positifs

[Fantino]

Non j'ai réussi à démontrer en supposant que Vn+1-Vn>0 on obtient un+1>=((n+1)/n)un
Comme un est croissante et que n+1/n tend vers 1 c'est bon.

[Lostounet]

Non j'ai réussi à démontrer en supposant que Vn+1-Vn>0 on obtient un+1>=((n+1)/n)un
Comme un est croissante et que n+1/n tend vers 1 c'est bon.

Euh.. a priori n est un entier naturel fixé.
Il n'a donc pas besoin de tendre vers quoi que ce soit..et on ne suppose pas Vn+1-Vn on le démontre...?

Il faut étudier uniquement le signe de V(n+1)-V(n) pour tout entier naturel n ...

[mehdi-128]

Bonjour
Soit u(n) avec n appartenant aux naturels non nuls
Si un est croissante prouvez que vn = (u1+u2+u3.... +un) /n est aussi croissante. J'ai vérifié cela avec tous types de suites (stationnaires,un<0....) mais je n'arrive pas à démontrer le cas général sans contraire une expression de un
Merci de votre aide

Par linéarité de la somme :



D'où :



Mais :

Ainsi :

[aviateur]

Vu que tu es bien lancé @mehdi tu peux finir?

[mehdi-128]

Salut Aviateur j'étais bloqué ici mais je viens d'avoir une idée



Or : (n termes)

D'où :

Par croissance de la suite on a :



Soit : par somme de termes positifs.

Par conséquent, comme on a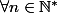



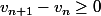
La suite est donc croissante.

[nodgim]

Remarque, avec Latex, ça en jette, c'est déjà ça.

[Fantino]

Merci beaucoup j'ai compris

[mehdi-128]

De rien ça me fait travailler moi aussi je prépare le CAPES seul chez moi.

[nodgim]

Ou plus simplement :

u1 < vn < un < u(n+1)

(n * vn + u(n+1)) / (n+1) = v (n+1) > (n * vn + vn) / (n+1) = vn