Critère de nullité

par **jeje56** » 23 Mai 2009, 13:51

Bonjour,

Je cherche une démo du critère de nullité pour une fonction polynôme :

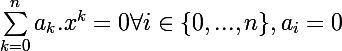
Le sens non direct est évident, mais pour le sens direct ?

Merci !

par **Maks** » 23 Mai 2009, 13:56

Bonjour,
Dérive !

par **jeje56** » 23 Mai 2009, 14:09

Je ne vois pas ce que ça peut me donner ?...

par **SimonB** » 23 Mai 2009, 14:14

jeje56 a écrit:Je ne vois pas ce que ça peut me donner ?...

Evaluer en 0 devrait te donner un des coefficients, et en dérivant, une récurrence apparaît.

par **Zweig** » 23 Mai 2009, 14:18

Salut,

Ca se fait aussi via les limites. On suppose

non nul. On divise le polynôme par

, on fait tendre

vers +oo et on obtient

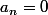
. On réitérant ce procédé, on montre que tous les

sont nuls.

par **Matt_01** » 23 Mai 2009, 14:22

Ou bien réfléchir sur le degré du polynôme tout simplement.

par **jeje56** » 23 Mai 2009, 14:52

SimonB a écrit:Evaluer en 0 devrait te donner un des coefficients, et en dérivant, une récurrence apparaît.

Slt,

L'évaluation donne a_0=0

Une évaluation en 0 de f' donne a_1=0
Pour la récurrence, elle se fait sur k ?

Merci !

par **abcd22** » 23 Mai 2009, 15:53

Bonjour,

jeje56 a écrit:Je cherche une démo du critère de nullité pour une fonction polynôme :

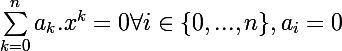
Si tu parles de nullité d'une fonction polynomiale, si les

sont dans un corps

, je suppose qu'il faut ajouter

au membre de gauche de léquivalence, et léquivalence nest vraie que si

est infini. Une technique qui marche pour tout corps k infini est de dire que le polynôme a plus de racines que son degré.

par **jeje56** » 23 Mai 2009, 17:36

abcd22 a écrit:Bonjour,

Si tu parles de nullité d'une fonction polynomiale, si les sont dans un corps , je suppose qu'il faut ajouter au membre de gauche de léquivalence, et léquivalence nest vraie que si est infini. Une technique qui marche pour tout corps k infini est de dire que le polynôme a plus de racines que son degré.

Oui pour tout x de K infini c'est vrai !
Mais pour le sens direct utiliser le nombre de racines me semble difficile non ?

par **jeje56** » 23 Mai 2009, 17:56

SimonB a écrit:Evaluer en 0 devrait te donner un des coefficients, et en dérivant, une récurrence apparaît.

Pour revenir à cette solution :

Supposons f(x)=0 pour tout x de K
f(0)=a_0=0

Soit P(i) la propriété :

donne en 0 : a_1=0
P(1) est vraie

Supposons P(i) vraie au rang i : a_i=0
Montrons P(i+1)

Est-ce la bonne méthode ici ?

Merci !

par **Maks** » 23 Mai 2009, 18:43

Je ne suis pas certain qu'une récurrence soit nécessaire.
Regarde. Je reprends tes notations.
Soit

.
La nullité de la dérivée

-ième te donne la nullité d'un coefficient. Puis tu réitères avec la derivée

-ième. Non ?

par **jeje56** » 23 Mai 2009, 19:01

Oui, c'est ce que je pensais : la récurrence ne me semble pas nécessaire... Pour tout i=0,...,n, la nullité de la dérivée i-ème donne la nullité du coefficient a_i... Est-ce vraiment une preuve ? Je dirais oui...

Edit : le seul pb est que je suis dans le cadre d'une leçon de capes et que la déf de la dérivée vient après ce critère dans mon plan... Est-ce gênant ?

par **Maks** » 23 Mai 2009, 21:04

Pourquoi ne serait-ce pas une preuve ?! Il faut bien le rédiger, c'est tout.
Sinon, sans la dérivée ... je ne vois pas comment faire !

par **abcd22** » 23 Mai 2009, 21:11

jeje56 a écrit:Mais pour le sens direct utiliser le nombre de racines me semble difficile non ?

Pour tout polynôme P sur un corps K et tout élément a de K, on a P(a) = 0 si et seulement si X - a divise P (car P = (X - a)Q + C avec C constante par division euclidienne, et en évaluant en a on trouve C = P(a)). Comme X - a et X - b sont premiers entre eux si a et b sont différents, si on prend n + 1 éléments distincts de K, on a

divise P...

par **leon1789** » 23 Mai 2009, 21:53

Si je peux me permettre, je soutiens à 100% la preuve de abcd22 :
elle est totalement algébrique (tout comme le résultat à démontrer) ;
elle est générale sur tout corps infini (et même tout anneau intègre infini) ;
elle "fournit" un contre-exemple sur les corps fini ;
elle n'utilise pas d'artifice comme la dérivation sur le corps particulier des nombres réels.
:zen:

par **jeje56** » 24 Mai 2009, 09:50

abcd22 a écrit:si on prend n + 1 éléments distincts de K, on a divise P...

Je suis d'accord, mais l'hypothèse est f=0 et on veut montrer que pour tout i, a_i=0... Là on tourne en rond non ?

Edit : à moins que P=0 ssi les a_i sont tous nuls est vrai par définition ? (P au sens du polynôme)

par **Zweig** » 24 Mai 2009, 10:59

Maks a écrit:Sinon, sans la dérivée ... je ne vois pas comment faire !

Voir mon message.

par **abcd22** » 24 Mai 2009, 11:56

jeje56 a écrit:Je suis d'accord, mais l'hypothèse est f=0 et on veut montrer que pour tout i, a_i=0... Là on tourne en rond non ?

Non, la définition de polynôme nul est « tous les coefficients sont nuls » comme tu le dis dans ton edit, et l'hypothèse de départ est « pour tout a, P(a) = 0 ».

par **jeje56** » 24 Mai 2009, 12:46

abcd22 a écrit:Non, la définition de polynôme nul est « tous les coefficients sont nuls » comme tu le dis dans ton edit, et l'hypothèse de départ est « pour tout a, P(a) = 0 ».

Oui je comprends, merci à toi ;-)

Critère de nullité

Critère de nullité

Qui est en ligne