Critère d'Eisenstein
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 12 Avr 2010, 10:35
par egan » 12 Avr 2010, 10:35
Salut tout le monde.
J'ai un petit problème en ce qui concerne la démo de ce critère.
La plupart connaisse la démo je suppose. Je vous dis juste où j'ai du mal.
A un moment on tombe sur:
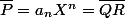
où
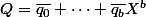
,
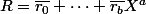
,
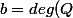 \geq 1)
et
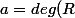 \geq 1)
.
On en déduit que
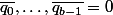
et
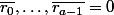
, ce qui permet de finir facilement la démo. C'est la que je bloque. Je vois pas du tout comment on en déduit ce truc là.
Merci d'avance.
@+ Boris.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Avr 2010, 10:49
par Ben314 » 12 Avr 2010, 10:49
Il te suffit de constater que, dans un produit QxR, on a :
terme_de_plus_bas_degré_de_QxR = terme_de_plus_bas_degré_de_Q x terme_de_plus_bas_degré_de_R
Or ici, terme_de_plus_bas_degré_de_QxR = anX^n donc...
(évidement, il faut aussi avoir vu que a+b=n)
En plus, je vois pas bien l'intérêt : si ta version du théorème est celle auquel je pense, la "déduction" r0=q0=0 [mod p] est sufisante pour conclure à une contradiction.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 12 Avr 2010, 11:12
par egan » 12 Avr 2010, 11:12
Ah oui d'accord.
Je ne comprennais pas non plus l'intérêt, c'est vrai qu'on en a pas besoin d'autant.
Merci beaucoup en tout cas. ^^
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 12 Avr 2010, 16:54
par egan » 12 Avr 2010, 16:54
Mais avec ce que tu dis, on a
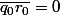
donc les deux ne sont pas forcément nuls ensemble. Mais c'est ce qu'il nous faut pour terminer. Je ne vois pas comment montrer que les deux sont nuls.
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 12 Avr 2010, 18:31
par egan » 12 Avr 2010, 18:31
Personne? :cry:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Avr 2010, 18:56
par Ben314 » 12 Avr 2010, 18:56
Si q0 était non nul (modulo p) alors, dans QR, le produit de q0 par le terme (non nul) de plus bas degré de R serait non nul et ce serait le seul de ce degré, donc on devrait avoir un terme de degrés inférieur ou égal à a dans P, ce qui n'est pas vu que a
Sinon, j'était en train de me dire que, si tu as fait deux sous de théorie sur les polynôme à coeff dans un corps quelconque, le poly P=anX^n de Fp[X] est déjà décomposé en produit de poly irréductible, donc s'il se factorise, c'est forcément à l'aide de poly de la forme cst.X^k
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 13 Avr 2010, 11:53
par egan » 13 Avr 2010, 11:53
Merci. ^^
C'est quoi Fp[X] ? Comme Z/pZ[X] mais dans un corps ?
Ce que tu veux dire c'est que X^n=X...X n fois.
Comme X est irréductible, X^n est décomposé en produit de polynômes irréductibles qui sont les polynômes X. Donc toute factorisation se fait en cste.X^k.
Vachement malin. ^^

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Avr 2010, 12:12
par Ben314 » 13 Avr 2010, 12:12
Pour
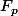
c'est juste une autre notation pour

(qui est bien un corps)
Aprés, pour la suite, c'est effectivement ça.
C'est effectivement "assez malin"... a condition d'avoir fait un peu la théorie sur les anneau (euclidiens) K[X] avec K corps quelconque pour pouvoir parler d'éléments irréductible là dedans.
L'autre méthode (avec les termes de plus bas degrés), à mon avis c'est au cas ou on ne sait pas que la notion de décomposition en facteurs irréductible fonctionne dans Fp[X].
Edit : En fait, vu l'énoncé qu'on cherche à montrer, y'a quand même intérêt à savoir un minimum ce que c'est qu'un polynôme irréductible !!!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 13 Avr 2010, 12:18
par egan » 13 Avr 2010, 12:18
Pour ce qui est de la méthode maline, ça correspond au cours sur les polynômes de MPSI ou alors j'ai loupé une subtilité ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Avr 2010, 12:32
par Ben314 » 13 Avr 2010, 12:32
J'sais pas, je connait pas les programmes...
La seule chose à savoir, c'est est-ce que le tout début du cours il commence par
"On se place dans K[X] avec K=R, C ou Q"
ou bien par
"On se place dans K[X] avec K un corps quelconque"
C'est pas complètement évident : lorsque l'on aborde la notion de dérivée (formelle) il se passe des trucs un peu différents dans les corps de caracéristique non nulle : par exemple, dans Z/pZ[X], le polynôme X^p (de degré p) a pour dérivée (formelle)... 0
Par contre, en ce qui concerne uniquement la théorie de la factorisation, il n'y a aucune différence (modulo le fait que, dans R ou C, les irréductibles se caractérisent trés simplement...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités